1. Геометрия
  2. Даны равнобедренный прямоугольный

Даны равнобедренный прямоугольный треугольник авс с прямым углом с, катетом ас=12см и квадрат сdef, такой, что две его стороны лежат на катетах, а вершина е на гипотенузе. найдите p квадрата.

MariaUralova MariaUralova    3   29.09.2019 06:40    19

Ответы
kimdana1 kimdana1  09.10.2020 02:09

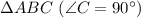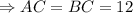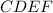Дано: \Delta ABC \ (\angle C = 90^{\circ}) - прямоугольный равнобедренный \Rightarrow AC = BC = 12 см; CDE F - квадрат.

Найти: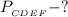 P_{_{CDE F}} - ?

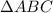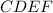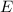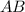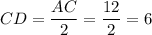Решение. Так как \Delta ABC прямоугольный равнобедренный при том, что у квадрата CDE F точка E лежит на гипотенузе AB, то эта точка делит эту гипотенузу пополам. Отсюда стороны квадрата CDE F делят катеты тоже пополам, то есть CD = \dfrac{AC}{2} = \dfrac{12}{2} = 6 см.

P_{_{CDE F}} = 4 \ \cdotp CD = 4 \ \cdotp 6 = 24 см.

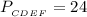ответ: P_{_{CDE F}} = 24 см.


Даны равнобедренный прямоугольный треугольник авс с прямым углом с, катетом ас=12см и квадрат сdef,
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
talex26052006в talex26052006в  29.01.2021 13:53
В зрізаному конусі R=16 cм, r=10 см, висота конуса 8 см. Знайти твірну зрізаного конуса Для розв язування задачi знадобиться розглянути осьовий перерiз зрiзаного конуса,...
1993nnnn 1993nnnn  29.01.2021 13:51
Көмектесндерш геометрия 3,29 есеп. ​...
Pars1fal Pars1fal  29.01.2021 13:51
Найдите сторону AB треугольника ABC, если AC=5, BC=4√2, угол C=45°​...
Spez18 Spez18  03.10.2019 22:40
Точка м не лежит в плоскости а докажите что все прямые проходящие через точку м и параллел плоскости а лежат в 1 плоскости ,...
Nanami334 Nanami334  03.10.2019 22:40
Вравнобедренном треугольнике abc угол c тупой, а угол a = 27 градусов. найдите угол b...
СВЕТЛАНУШЕНЬКА СВЕТЛАНУШЕНЬКА  03.10.2019 22:40
Длина окружности, описанной около равнобедренного треугольника, равна 120π см. найти периметр этого треугольника, если высота, проведенная к основанию 48 см....
ruqiyaaminova1 ruqiyaaminova1  03.10.2019 22:40
Какая последовательность не является прогрессией? 3, 6, 9, 12 2, 6, 18, 54 1, 5, 25, 125 4, 8, 16, 32...
KSUmaUYouTobe KSUmaUYouTobe  18.10.2020 10:34
Ушбурыштын орты сызыгы одан буиыр кабыргалары 11дм жане 15дм жане кышы табаны 9дм болатын трапеция киып тусыреды ушбурыштан периметрын табыныздар...
barinovasonya0p00t3v barinovasonya0p00t3v  05.05.2020 12:19
2) AB - диаметр окружности с центром О. Найдите координаты центра окружности, если А(1;-3) и В(5;-1)b) Запишите уравнение данной окружности3) выполнить построение двух окружностей,...
Сaшкa12 Сaшкa12  05.05.2020 12:19
В чотирикутнику АВСD (BC ІІ AD) ВС=8 см, а бісектриса кута D потрапляє в точку B і утворює зі стороною BC кут у 30 градусів, а з боковою стороною AB кут у 90 градусів. Знайдіть...

Популярные вопросы