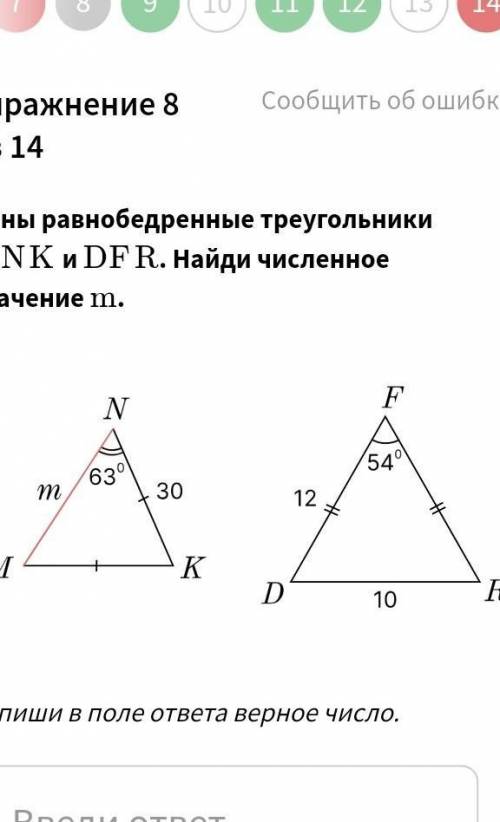
Даны равнобедренные треугольники MNK MNK и DFRDFR. Найди численное значение mm.

m=25.

Объяснение:

Решение на фотографии.

Для решения данной задачи, нам необходимо использовать свойства равнобедренных треугольников.

Первое свойство, о котором нам следует помнить, это то, что у равнобедренного треугольника два равных угла и две равные стороны. В данном случае, у треугольника MNK, имеющего основание MN и боковые стороны MK и NK, углы MNK и KNM равны, а стороны MK и NK также равны.

Другое свойство, которое нужно учитывать, это то, что вершины противоположным сторон углов равнобедренного треугольника делят его на два равных треугольника. В нашем случае, треугольник DFR делится вершиной R на два равных треугольника DFR и FDR.

Теперь рассмотрим треугольник DFR. Мы знаем, что у этого треугольника угол FDR равен углу MNK, так как они являются одними из равных углов равнобедренных треугольников. Это означает, что уголы DFR и KNM также равны.

Теперь мы можем заметить, что у нас есть два треугольника DFR и MKN, у которых соответствующие углы равны. Поэтому эти треугольники подобны.

Подобные треугольники имеют пропорциональные стороны. То есть, отношение длины стороны DF к длине стороны MK равно отношению длины стороны FR к длине стороны NK:

DF/MK = FR/NK

Теперь мы можем воспользоваться данной пропорцией для определения значения mm.

Из задания нам известно, что DF = 19 см, MK = 8 см и FR = 38 см. Мы не знаем значение стороны NK, но можем обозначить его как m.

Записав пропорцию и подставив известные значения, получим:

19/8 = 38/m

Теперь нам нужно решить эту пропорцию относительно m. Для этого мы можем использовать правило трех (произведение крест на крест):

19m = 8 * 38

Теперь решим получившееся уравнение:

19m = 304

m = 304/19

m = 16

Таким образом, численное значение mm равно 16 см.