Даны плоскость 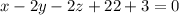 , прямая
, прямая 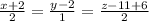 и точка
и точка 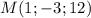 .Найти уравнение прямой, проходящей через точку M параллельно заданной плоскости так, чтобы она пересекала данную прямую и найти эту точку пересечения.
.Найти уравнение прямой, проходящей через точку M параллельно заданной плоскости так, чтобы она пересекала данную прямую и найти эту точку пересечения.
Другие вопросы по теме Геометрия
Популярные вопросы
- Определить эквивалент H2So4...
2 - 2 Задание. Укажите на карте: ( ) 1. Три ярмарки, существовавшие в...
3 - Заполните таблицу- Источники, функции и признаки недостаточности...
2 - Сеть питания пресного водоёма...
2 - Д.Исабеков Әпке драмасының көркемдік идеялық қундылығын гуманистік...
1 - Кто может . Выпишите прилагательные с существительными укажите род,...
3 - 10. Берілген суретті пайдаланып , тыныс алганда жане тыныс шыгарганы...
3 - Англію якої доби зобразив Льюїс Керролл у книжці «Аліса в Країні...
1 - 40б конспект по теме Батыево нашествие на русь полный по учебнику...
3 - 3. Путь от пункта А до пункта В велосипедист проехал за 6 ч, а мотоциклист...
2
1. Найдем вектор нормали плоскости:
Уравнение плоскости дано в общем виде: x - 2y - 2z + 22 + 3 = 0.
Нормальный вектор плоскости задается коэффициентами при x, y, z:
n = (1, -2, -2).
2. Найдем направляющий вектор прямой:
Уравнение прямой дано в параметрической форме: x/2 = (y-2)/1 = (z-11+6)/2.
Направляющий вектор прямой выражается через коэффициенты в уравнении, стоящие перед x, y, z:
v = (2, 1, 2).
3. Найдем уравнение прямой:
Так как прямая должна быть параллельна плоскости, то ее вектор направляющий должен быть коллинеарен вектору нормали плоскости. Для этого, разделим компоненты вектора направляющего на соответствующие компоненты вектора нормали и найдем общий множитель:
k = 2/1 = 1/-2 = 2/-2 = -1.
Таким образом, уравнение прямой имеет вид:
x = 1 + 2t,
y = -3 + t,
z = 12 + 2t,
где t - параметр.
4. Найдем точку пересечения прямой и заданной прямой:
Подставим параметрические уравнения прямой в уравнение заданной прямой и найдем значение параметра t:
(1 + 2t)/2 = (-3 + t - 2)/1 = (12 + 2t - 11 + 6)/2.
Решим полученную систему уравнений, подставив значение t в одно из уравнений и найдем координаты точки пересечения.
Для примера, возьмем первые два уравнения:
(1 + 2t)/2 = (-3 + t - 2)/1,
(1 + 2t)/2 = (t - 5)/1,
1 + 2t = 2t - 10,
1 = -10.
Получили противоречие, значит, точки пересечения нет.
Это означает, что заданная прямая и искомая прямая не пересекаются.
Итак, уравнение прямой, проходящей через точку M параллельно заданной плоскости, имеет вид:
x = 1 + 2t,
y = -3 + t,
z = 12 + 2t.
Точки пересечения заданной прямой и искомой прямой не существует.