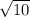Даны координаты вершин треугольника (6;-9) (10;-1) (-4;1) . Найти: 1. Уравнения прямы. проходящих через вершины треугольника.
2. Уравнения медиан треугольника
3. Уравнения высот треугольника.
4. Точку пересечения медианы. проведенной из вершины А и высоты, проведенной из вершины В.
5. Тангенсы углов треугольника.

1. Прямая ВC формула прямой у=(3-х)/7

Прямая АВ формула прямой у=2х-21

Прямая АС формула прямой у= -х-3

2. у=9-3х  медиана  АА1

у=1/3х-39/9 - медиана ВВ1

у= -0,5х-1 - медиана СС1

3. у(АА2)=7,1х-51,5

ВВ2 высота у=х-11

СС2 уравнение  у= -0,5х-1

4. А3(5;-6) т пересечения медианы АА1 и высоты ВВ2

5.tg∠A=3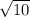

tg∠B=tg∠A

tg∠C=2/3/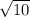

Объяснение:

1. Коэфициент при х - это (у-уо)/х т.В(10;-1)

для ВС (у-уо)/х=(-1+21)/10=2

2. АА1 - медиана Определим координаты А1(3; 0)

уравнение медианы АА1

у=9-3х

ВВ1 - медиана В1(1; -4)

у=1/3х-39/9

СС1 С1 (8; -5)

у= -0,5х-1

3.АА2 высота

А2 (7,2; -0,6)

у(АА2)=8,5/1,2х-61,8/1,2=7,1х-51,5

ВВ2 высота

координата В2=(4; -7)

у=х-11

СС2 тС2=С1 (8; -5)

у= -0,5х-1

5. tg∠A=CC1/AC1

Определяем модули векторов СС1 (12;-6) и АС1 (2;4)

tg∠A=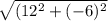/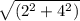=3

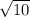
tg∠B=tg∠A

tg∠C=2*AC1/CC1=2*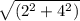/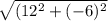=2/3/