Даны координаты вершии теугольника авс,найти;

1)длины сторо ав ас вс

2)уравнение высаты,проведенный через вершинус

3)уравнение прямой ав

4)угол между векторами ав иас

а(1; 5) в(2; -4) с(0; 1)

Объяснение:

1) длины сторон АВ АС ВС

считаются по формуле  

 .

Давайте рассмотрим на примере АВ.

А(1;5) В(2;-4)  

АВ=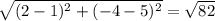

2) уравнение прямой, проходящей через две точки с координатами А(х1,у1) и В(х2, у2) находится по формуле

Подставляем наши значения

-9x+6=y

коэффициенты прямой k1=-9, b1=6

Проделав то же самое, но для прямой по координатам отрезка АС найдем

у=4х+1 , k2=4, b1=1

3) зная два уравнения прямых мы сможем найти угол, которые они образуют при пересечении

tgα=13/35 ⇒ arctg13/35 ≈ 20°

3) УРАВНЕНИЕ ВЫСОТЫ, проведенной через вершину С

Прямая, к которой проведен перпендикуляр описывается уравнением -9x+6=y

k1=-9

Для двух ⊥-ых прямых должно выполняться условие k1*k2=1

т/е подбираем коэффициент  k2 для уравнения высоты, поскольку высота треугольника это перпендикуляр, опущенный из вершины. Несложно догадаться, что k2 будет -1/9

Прямая, проходящая  через точку N0 (х0, у0)( в нашем случае это С (0, 1) описывается уравнением:

.

или