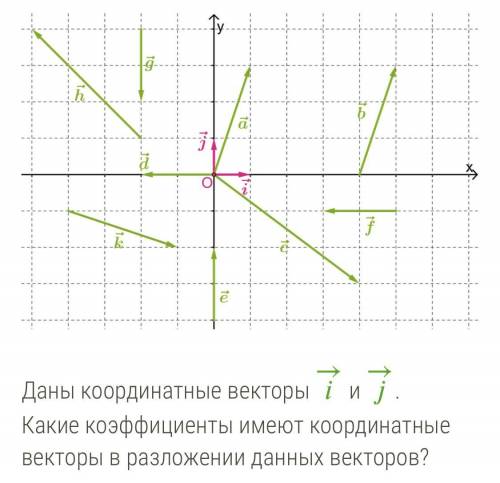
Даны координатные векторы i и j. Какие коэффициенты имеют координатные векторы в разложение данных векторов?

Данный вопрос связан с линейной алгеброй и векторами. Для того чтобы ответить на него, необходимо разобраться с понятием координатного вектора и его разложением.

Координатные векторы обычно обозначаются буквами i и j. В данном случае i - это вектор, который указывает направление и длину от точки А до точки В. Аналогично, j - это вектор, который указывает направление и длину от точки А до точки С.

Для разложения векторов i и j на координаты, мы можем воспользоваться правилом параллелограмма, которое говорит о том, что векторная сумма двух векторов равна стороне параллелограмма, проведенной между началом и концом этих векторов.

Чтобы разложить вектор i на координатные векторы, мы проводим перпендикуляр из точки В на ось АС. Пусть точка, в которой этот перпендикуляр пересекает ось АС, будет называться D. Тогда, вектор i будем разлагать на два вектора: АД и ДВ.

Для разложения вектора j на координатные векторы, мы проводим перпендикуляр из точки С на ось АВ. Пусть точка, в которой этот перпендикуляр пересекает ось АВ, будет называться Е. Тогда, вектор j будем разлагать на два вектора: АЕ и ЕС.

Теперь рассмотрим координаты разложенных векторов. Пусть точка А имеет координаты (0, 0), точка В - (x1, 0), точка С - (0, y1), точка D - (x1, y1), точка E - (x2, y1). Тогда, координатный вектор АД будет равен (x1, y1), координатный вектор ДВ - (0, -y1), координатный вектор АЕ - (x2, 0), координатный вектор ЕС - (-x2, y1).

Таким образом, координатные векторы в разложении данных векторов имеют следующие коэффициенты:
- Координатный вектор i разлагается на два вектора: (x1, y1) и (0, -y1).
- Координатный вектор j разлагается на два вектора: (x2, 0) и (-x2, y1).

Ответ можно представить в виде таблицы:
```
| Вектор | Координаты |
|--------|------------|
| i | (x1, y1) |
| | (0, -y1) |
| j | (x2, 0) |
| | (-x2, y1) |
```

Надеюсь, это подробное и пошаговое объяснение помогло вам понять, какие коэффициенты имеют координатные векторы в разложении данных векторов. Если у вас возникнут еще вопросы, не стесняйтесь задавать.