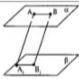
Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А1 и В1. Найдите длину отрезка А1 В1 если АВ = 10 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Укажіть речення, але не вжито вставие славе (разділові знаки...
2 - ПОМАГИТЕ ЭТО СОЧ Nº1.Choose correct forin of comparative and superlative...
3 - По рис. 34 и 35 (учебник, стр. 63, 64) сравните три изображения...
3 - Составные части земной коры? а)магма, осадочные,метаморфические...
1 - Знайдіть площу земельної ділянки прямокутної форми з вимірами...
3 - Прочитать главы из Детства Тёмы Н.Г.Гарин-Михайловского Иванов...
1 - Жамбыл менің жай атым, халық менің шын атым тақырыбында эссе...
2 - Напишите даю 100-150 слов...
2 - Запишите уравнения реакций, при которых можно осуществить превращения....
3 - 1. Оформи предложение грамматически правильно: расставь знаки...
3
Однако перед тем, как решить задачу, давайте проанализируем данное условие.
У нас есть две параллельные плоскости (плоскость, в которой лежат точки А и В, и вторая параллельная плоскость). Мы требуем, чтобы А1В1 находилось на первой плоскости. Для этого, мы можем провести отрезки А1С и В1D перпендикулярно к плоскости, где А1В1 находится, и которые пересекают вторую параллельную плоскость в точках С и D соответственно.
Теперь, когда у нас есть такая система, мы можем применить подобие треугольников. Треугольники А1В1С и АВС подобны, потому что углы между параллельными прямыми одинаковые (они вертикальные и поперечный уголов), а углы между перпендикулярными прямыми одинаковые (они прямые углы).
У нас есть данная информация: АВ = 10 см. Давайте обозначим длину отрезка А1В1 как х.
Поскольку треугольники АВС и А1В1С подобны, мы можем записать пропорцию длин сторон:
АВ/А1В1 = AC/А1С
Теперь, давайте подставим известные значения в пропорцию:
10/х = 10/С
Обратите внимание, что длины АВ и С пропорциональны. Это означает, что если одна длина увеличивается в 2 раза, другая длина тоже увеличивается в 2 раза.
Таким образом, если АВ равно 10 см, то С равно х, и мы можем записать новую пропорцию:
10/х = 10/10
Теперь мы можем упростить пропорцию:
10/х = 1
Поделим обе стороны на 10:
1/х = 1/10
Теперь, чтобы избавиться от дроби, мы можем умножить обе стороны на 10х:
10 = х
Таким образом, длина отрезка А1В1 равна 10 см.
Итак, ответ: длина отрезка А1В1 равна 10 см.