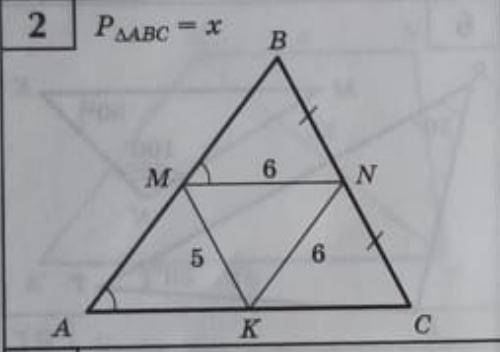
Дано: в треугольнике ABC угол MAK = углу BMN, BN = NC, MN = 6, NK = 6, MK = 5. Найти: площадь треугольника ABC

Для решения этой задачи, мы можем использовать несколько различных методов, например, так:

Метод 1: Использование понятия равенства треугольников

1. Обратим внимание на углы MAK и BMN - у них есть совпадающая сторона MK и нам дано, что эти углы равны. Поэтому треугольники MAK и BMN равны.
2. Это означает, что стороны MA и MB также равны, потому что углы M равны и MK - общая сторона.
3. Аналогично, мы можем сделать вывод, что треугольники NKC и NBM равны, поскольку у них есть одна общая сторона и равные углы NBC и NCB.
4. Следовательно, стороны NC и NB, а также NK и NM равны.

Метод 2: Использование формулы площади треугольника

5. Обратим внимание, что треугольник ABC имеет сторону NC, равную стороне BN, и сторону AC, равную стороне BC. Поэтому треугольник ABC - равнобедренный.

6. Мы можем найти высоту треугольника MBN, проведя перпендикулярной к стороне BN из вершины M. Назовем эту высоту h. Мы знаем, что MK = 5 и NK = 6.

7. Используя теорему Пифагора в треугольнике MKB, мы можем найти длину стороны MB: MB^2 = MK^2 - BK^2. Подставляя известные значения, получим MB^2 = 5^2 - 6^2 = 25 - 36 = -11. Поскольку MB^2 отрицательно, мы должны исключить этот вариант. Значит, высота h будет нулевой.

8. Мы можем найти высоту треугольника NBC, проведя перпендикулярной к стороне NC из вершины N. Назовем эту высоту h'. Мы знаем, что NK = 6 и MK = 5.

9. Используя теорему Пифагора в треугольнике NKB, мы можем найти длину стороны NB: NB^2 = NK^2 - KB^2. Подставляя известные значения, получим NB^2 = 6^2 - 5^2 = 36 - 25 = 11. Значит, NB = √11.

10. Мы знаем, что высота h' равна расстоянию от вершины N до стороны AC, и она составляет отношение √11/2.

11. Используя формулу площади треугольника, S = (основание * высота) / 2, мы можем найти площадь треугольника ABC: S = (AB * h') / 2. Подставляя известные значения, получим S = (√11 * √11/2) / 2 = 11/2.

Ответ: Площадь треугольника ABC равна 11/2.