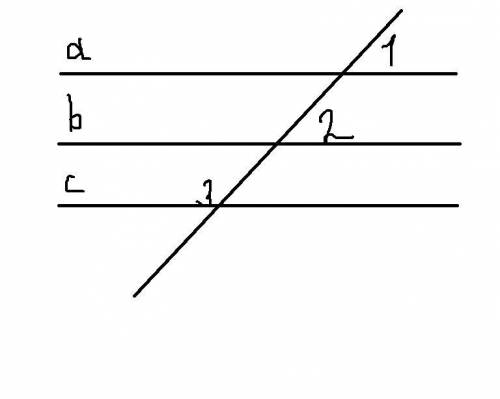
Дано угол1=углу2, угол2+угол3+180(градусов)
Док-ть a Параллельна c

Данный вопрос требует доказательства, что отрезок 'a' параллелен отрезку 'c', при условии, что угол 1 равен углу 2 и сумма угла 2, угла 3 и 180 градусов.

Для начала, давайте разберемся с основными понятиями. Параллельные прямые - это прямые, которые никогда не пересекаются и всегда находятся на одинаковом расстоянии друг от друга. Чтобы доказать, что отрезок 'a' параллелен отрезку 'c', мы должны показать, что углы между этими отрезками равны.

Дано: угол 1 = угол 2, угол 2 + угол 3 + 180 градусов.

1. Рассмотрим треугольник ABC. У нас есть две пары равных углов (условие угол 1 = угол 2), поэтому этот треугольник является равнобедренным.

2. Одна пара оснований равнобедренного треугольника BC и AC (отрезки 'b' и 'c').

3. Предположим, что отрезок 'a' не параллелен 'c'. Тогда у нас будут образовываться перпендикулярные линии и углы между отрезками будут разными.

4. Давайте рассмотрим угол 3 и угол A в треугольнике ABC. По условию угол A равен углу 2. Если 'a' и 'c' не параллельны, то угол 3 и угол A будут разными.

5. Но по условию у нас есть сумма угла 2, угла 3 и 180 градусов. Значит, угол 3 и угол A равны.

6. Поскольку угол A и угол A' (обратный угол A) равны, а угол 3 и угол A равны, то в равнобедренном треугольнике угол A и угол A' также должны быть равны.

7. Поэтому отрезок 'a' должен быть параллелен отрезку 'c', так как углы между ними равны.

Таким образом, мы доказали, что если угол 1 равен углу 2 и угол 2 + угол 3 + 180 градусов, то отрезок 'a' параллелен отрезку 'c'.