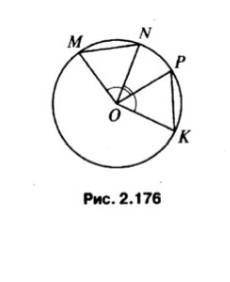
Дано: угол MOP=угл NOK Доказать: MN=PK​

Для решения данной задачи нам понадобится использовать две важные теоремы о равенстве углов: теорему о вертикальных углах и теорему о равных углах, образованных пересекающимися прямыми.

По условию задачи, угол MOP равен углу NOK. Обозначим этот равный угол через "а".

Используя теорему о вертикальных углах, мы знаем, что угол MOR также равен углу NOK. Обозначим этот угол через "а".

Таким образом, угол MOR равен MOP, а угол NOK равен MOP. Мы можем обозначить их равенство следующим образом:

MOR = MOP = NOK = а

Теперь рассмотрим треугольник MNK. Сумма углов в треугольнике равна 180 градусов, поэтому:

M + N + K = 180

Заметим, что угол MOP является внутренним углом треугольника MNK, а равные внутренние углы треугольника равны. Таким образом, угол NOK также равен MOP, то есть "а".

M = а

Подставляем эти значения в уравнение суммы углов треугольника:

M + N + K = а + N + K = 180

После вычитания (N + K) из обеих сторон получаем:

а = 180 - N - K

Теперь мы можем заметить следующее: углы M и P образуют сворачивающиеся лучи, значит, они также равны. Обозначим этот угол через "в".

P = в

Так как угол MOP является прямым углом, его величина равна 90 градусов:

в = 90

Теперь у нас есть два равных угла: угол MOP, который равен а, и угол P, который равен в. Поэтому:

а = в = 90

Таким образом, мы доказали, что угол P равен 90 градусов.

Теперь рассмотрим треугольники MNP и PKO. У них есть две равных стороны: MN и PK, а также одинаковый угол NMP, который равен углу OKP (поскольку они вертикальные).

Используя теорему о равенстве треугольников (SSS), мы можем сделать вывод, что эти два треугольника равны:

МН = PK

Таким образом, мы доказали, что стороны MN и PK равны.

Вот ответ на задачу: MN = PK.