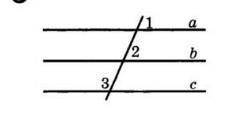
Дано: угол 1=углу 2, угол 2+ угол 3=180
Доказать, что a параллельна c :)

Для доказательства того, что линия a параллельна линии c, мы можем использовать признаки параллельности углов.

Исходя из условия задачи, у нас есть две важные информации: угол 1 равен углу 2 и угол 2 плюс угол 3 равно 180 градусов.

Для начала, давайте обратимся к первому условию - угол 1 равен углу 2. Это означает, что эти два угла являются вертикальными углами. Из свойств вертикальных углов следует, что они равны между собой. Таким образом, угол 2 равен углу 1.

Далее, обратимся ко второму условию - угол 2 плюс угол 3 равно 180 градусов. Это означает, что уголы 2 и 3 являются смежными углами и вместе образуют линейный угол. Из свойств линейных углов следует, что сумма всех углов линейного угла равна 180 градусов. Таким образом, угол 2 плюс угол 3 равно 180 градусов.

Теперь мы можем сделать вывод, что угол 1 равен углу 2, который равен углу, состоящему из угла 2 и угла 3. В данном случае, угол 1 равен углу 2, а угол 2 плюс угол 3 также равно 180 градусов. Это означает, что угол 1 равен углу, состоящему из угла 2 и угла 3.

Теперь давайте рассмотрим линии a и c. Мы знаем, что угол 1 равен углу, состоящему из угла 2 и угла 3. Из свойства вертикальных углов следует, что угол 1 также равен углу, образованному линией a и линией c (поскольку эти два угла являются вертикальными углами).

Таким образом, мы можем заключить, что угол, образованный линией a и линией c, равен углу 1, который равен углу, состоящему из угла 2 и угла 3. Следовательно, угол, образованный линией a и линией c, равен углу, состоящему из угла 2 и угла 3.

Из этого можно сделать вывод, что линия a параллельна линии c, так как углы, образованные этими линиями, равны между собой. Это вывод основан на признаке параллельности углов.

Таким образом, доказательство данного утверждения состоит в том, что угол 1 равен углу 2, угол 2 плюс угол 3 равно 180 градусов, а угол, образованный линией a и линией c, равен углу, состоящему из угла 2 и угла 3. Это означает, что линия a параллельна линии c.