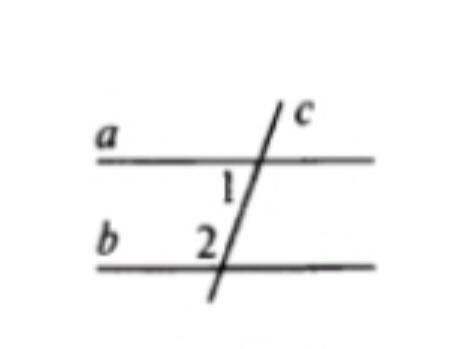
Дано: угол 1=48градусов, угол2=132градуса Доказать: а||b

распишите подробно: Дано:..
Доказать:..
Доказательство:..

Дано: угол 1 = 48 градусов, угол 2 = 132 градуса
Доказать: а || b

Для доказательства параллельности линий а и b, мы должны использовать свойство углов при пересечении прямых. Если сумма внутренних углов, образованных двумя прямыми и пересекающей их третьей прямой равна 180 градусам, то прямые а и b будут параллельными.

Дана следующая информация:
Угол 1 = 48 градусов
Угол 2 = 132 градуса

Для начала, давайте рассмотрим свойство суммы углов. Угол 1 и угол 2 образуют пару внутренних углов при пересечении двух прямых (a и b) третьей прямой (пунктирной линией). Следовательно, сумма углов 1 и 2 должна быть равна 180 градусам.

Угол 1 + Угол 2 = 48 + 132 = 180

Так как сумма углов 1 и 2 равна 180 градусам, мы можем заключить, что прямые а и b параллельны. В данном случае, прямые а и b обозначены как линии, которые пересекаются и образуют равные углы.

Таким образом, основываясь на свойстве суммы углов при пересечении прямых, мы можем заключить, что а и b параллельны.

Обоснование ответа:
Мы использовали свойство суммы углов при пересечении прямых, которое устанавливает, что если сумма внутренних углов, образованных двумя прямыми и пересекающей их третьей прямой, равна 180 градусам, то прямые а и b параллельны.

Пошаговое решение:
1. Проверить, какие углы даны и какие требуется доказать.
2. Применить свойство суммы углов при пересечении прямых, которое устанавливает, что их сумма должна быть равной 180 градусам.
3. Просуммировать углы 1 и 2.
4. Если сумма углов равна 180 градусам, то можно заключить, что прямые а и b параллельны.
5. Обосновать ответ, ссылаясь на использованное свойство суммы углов при пересечении прямых.