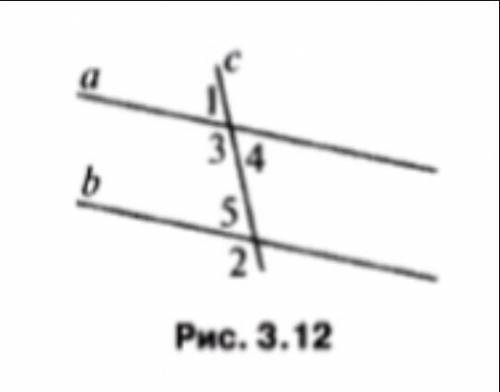
Дано: угол 1=47 градусов, угол 2=133градуса Доказать: a||b

, нужно ПОДРОБНО расписать ЧЕРЕЗ ДАНО

/_ у нас это значок угла

|| у нас это будет значок параллельности

1)  /_3=180°-/_1=180°-47° это  смежных углов свойство.

2) /_2 и /_3 - равные углы, образованные секущей c при прямых a и b, а значит a||b по 2-ому признаку параллельности прямых у нас это если е углы равны, тогда у нас будут прямые  параллельны.

Объяснение:

Чтобы доказать, что прямые a и b параллельны, мы должны использовать вспомогательную прямую c.

Дано, что угол 1 равен 47 градусов, а угол 2 равен 133 градуса.

1. Построим вспомогательную прямую c, которая пересекает прямые a и b.
2. Пометим точку M на прямой c так, чтобы угол 1 был равен углу, образованному прямой a и прямой c.
3. Пометим точку N на прямой c так, чтобы угол 2 был равен углу, образованному прямой b и прямой c.
4. Соединим точки M и N с вершиной A угла 1 и точкой B угла 2 соответственно. Таким образом, мы построили два треугольника: треугольник AMB и треугольник ANB.
5. Поскольку углы AMB и ANB равны соответственно углам 1 и 2, то этот факт нам говорит о равенстве углов AMB и ANB.
6. Рассмотрим две части треугольника AMB: AM и MB.
7. Из теоремы о сумме углов треугольника известно, что сумма углов треугольника равна 180 градусов.
8. Заметим, что AMB и ANB – это две части одного и того же треугольника ABM. Поэтому сумма углов AMB и ANB равна углу ABM.
9. Поэтому сумма углов AMB и ABM равна 180 градусов.
10. Из пункта 9 мы можем заключить, что угол ABM равен 133 градуса (по условию).
11. Также, углы AMB и ABM равны (из пункта 5).
12. Из пункта 11 и симметрии углов следует, что угол MAB равен 133 градуса.
13. Заметим, что угол 1, угол MAB и угол ABM – это три угла, образованные прямой a и прямой c. То есть, уголы MAB и 1 равны.
14. Аналогично, угол NAB равен углу 2.
15. Из пункта 13 мы можем заключить, что угол 1 равен углу MAB, а угол 2 равен углу NAB.
16. Теперь обратимся к треугольнику ANB. Заметим, что два угла этого треугольника (угол NAB и угол ANB) равны. Поэтому угол 2 равен углу ANB.
17. Из пункта 16 следует, что углы 1 и 2 равны углам ANB и NAB соответственно.
18. Отсюда следует, что углы ANB и NAB равны.
19. Используя свойство параллельных прямых, мы знаем, что у параллельных прямых углы, образованные ими и пересекающейся прямой, равны.
20. Таким образом, поскольку угол ANB равен углу NAB, и угол AMB равен углу 1, мы можем заключить, что прямые a и b параллельны.

Таким образом, мы доказали, что прямые a и b параллельны, используя все данное и все шаги рассуждений.