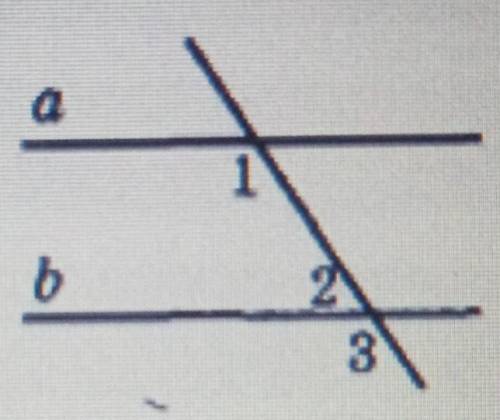
Дано: угол 1= 120°, угол 3 = 2* 2
Параллельны ли а и б
​

Для того чтобы определить, параллельны ли прямые "а" и "б", нам необходимо учесть несколько правил геометрии.

1. Углы, образованные параллельными прямыми и пересекающей их третьей прямой, называются соответственными углами.

2. Соответственные углы равны между собой.

3. Углы, дополнительные к одному и тому же углу, равны между собой.

Теперь давайте рассмотрим данную задачу:

Угол 1 изображен треугольником с основанием, являющимся прямой "а". Угол 1 равен 120°.

Угол 2 и угол 3 также получены при пересечении параллельных прямых "а" и "б" третьей прямой. Угол 3 изображен треугольником с основанием, являющимся прямой "б". Угол 3 равен углу 2 умноженному на 2.

Из задачи не ясно, какое значение имеет угол 2, поэтому мы не можем точно сказать, равны или не равны углы 1 и 3. Ответ на вопрос о параллельности прямых "а" и "б" не может быть определен только на основании данной информации.

Дополнительные данные о значениях угла 2 и оснований прямых "а" и "б" нужны для решения этой задачи.