Дано: треугольник авс, т.а(-12,2) в(4,8) с (4,-4) док-ть что треугольник авс равнобедренный

Ответы

SerenaWilliamsisa 26.05.2020 11:21

по формуле расстояния между двумя точками, заданными координатами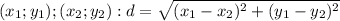 $(x_1;y_1); (x_2; y_2): d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

находим длины сторон треугольника АВС

$AB=\sqrt{(-12-4)^2+(2-8)^2}=\sqrt{16^2+6^2}=\sqrt{292}=2\sqrt{73};\\ BC=\sqrt{(4-4)^2+(8-(-4))^2}=\sqrt{0^2+12^2}=12;\\ AC=\sqrt{(-12-4)^2+(2-(-4))^2}=\sqrt{16^2+6^2}=\sqrt{292}=2\sqrt{73};$

AB=AC - значит треугольник АВС равнобедренный (по оперделению равнобедренного треугольника)

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

kektuber222owf6bv 05.02.2022 19:28

Основи ривнобичнои трапеции доривнують 16см та 40 см.Бични сторони доривнують по 20 см.Знайдить висоту....

ailchencko2010 05.02.2022 19:32

На рисунке AB : AD = AC : AE = BC : ED. Это означает, что угол ABC подобен ... и угол ABC = углу ...; угол ВСА = углу ......

kazorinJeka 05.02.2022 19:33

Бісектриса трикутника ділить сторону на відрізки, різниця яких 1 см. Знайдіть периметр трикутника,якщо дві інші його сторони 10 і 8 см...

tamtamtamira 05.02.2022 19:34

Определите вид ушла М треугольника МТС...

matievskaya79 05.02.2022 19:40

Два параллельные прямые a и b пересекают третья прямая c. если ∢2=51, то...

vasa2283 05.02.2022 19:41

Дано:Кут1=кут2;кут3=кут4 довести що ABC=ADC...

marina8marta 12.07.2019 12:17

Свойство углов четырёхугольника вписанного в оуружность из билета по ! ...

школа5553 12.07.2019 12:21

Знайти об єм правильної чотирикутної піраміди висота якої 8 см а бічне ребро 17 см...

hodyukmaria 12.07.2019 12:24

Площа основи косинуса 64п см^2 h=15 см sб-?...

as79118487190 12.07.2019 12:28

Катет прямокутного трикутника дорівнює 20см а його проекція на гіпотенузу 16 см зн гіпотенузу...

Дано: треугольник авс, т.а(-12,2) в(4,8) с (4,-4) док-ть что треугольник авс равнобедренный

Популярные вопросы