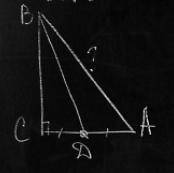
Дано: Треугольник ABC , Угол С = 90°. АС = 8 см, медиана BD = 2*√13см Найти AB

10 см

Объяснение:

Дано: ΔАВС - прямоугольный, ∠С=90°,  ВD - медиана, BD=2√13 cм, АС=8 см.    АВ - ?

Если в условии дана медиана треугольника, я решаю задачу, достроив треугольник до параллелограмма.  Теорема об удвоении медианы:

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Продлеваем медиану на такую же длину и строим параллелограмм АВСК, где диагональ АС=8 см, диагональ ВК=2√13+2√13=4√13 см.

Тогда АС²+ВК²=2(АВ²+ВС²).

208+64=2(АВ²+ВС²)

272=2(АВ²+ВС²)

АВ²+ВС²=136.

Вернемся к ΔАВС. По теореме Пифагора

АВ²+ВС²=136

АВ²-ВС²=64 (т.е. АС²)

2АВ²  =  200;  АВ²=100;  АВ=10 см.

СД=АД=4см

ВС=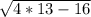=√36=6см

АВ=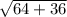=√100=10см

Объяснение: