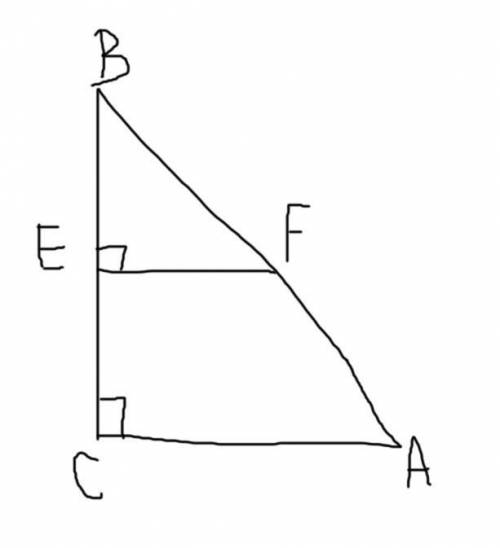
Дано: треугольник ABC, угол A = 90 градусов, EF || AC, AC = 28, EF=7, CE=14. Найти: BC.
Другие вопросы по теме Геометрия
Популярные вопросы
- Диаметр цилиндра равен 6 м, высота равна радиусу. найдите площадь полной...
1 - Постройте график функции у=х^2 на заданном промежутке. а) (- бесконечность;...
1 - На двух бензозаправочных станциях было 177 ц бензина.после того как на одной...
1 - Можно ли использовать словосочетание фруктовый садик ...
1 - Выпиши два слова в которых одинаковое количество гласных и согласных букв.весной,...
2 - Основные требования при проведении опроса...
1 - Стих бережное отношение к природе...
3 - Название отряда - тема будущее...
3 - Диафантовые уравнения 23x+4y-7x=-3y+15 31x+28y=1460 87x-64y=3 56x+72y=40...
1 - Вкниге три повести .в первой повести 80 страниц,во второй 60 страниц, а в...
2
У нас есть треугольник ABC, где угол A равен 90 градусов. Также дано, что EF параллельна AC, AC равно 28, EF равно 7 и CE равно 14.
Первым шагом, давайте определим, какие стороны и углы нам известны. У нас есть угол A равный 90 градусов, что делает треугольник прямоугольным. Мы знаем, что AC равно 28 и EF равно 7.
Далее, вспомним свойства параллельных линий. Мы знаем, что EF параллельна AC. Значит, угол B равен углу FCE. Также, угол B равен углу A, так как треугольник ABC является прямоугольным.
Возвращаясь к треугольнику FCE, мы видим, что у нас есть две известные стороны - CE равно 14 и EF равно 7. Мы можем использовать теорему Пифагора, чтобы найти длину стороны FC.
Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Применяя теорему Пифагора к треугольнику FCE, мы можем записать следующее уравнение:
CE² + FC² = FE²
14² + FC² = 7²
196 + FC² = 49
Теперь мы можем решить это уравнение, вычитая 196 с обеих сторон:
FC² = 49 - 196
FC² = -147
Мы получили отрицательное число, что значит, что длина стороны FC мнимая (несуществующая), что не имеет смысла в данной ситуации. Это означает, что треугольник невозможно построить с заданными размерами.
Таким образом, ответ на задачу "найти BC" - невозможно найти длину стороны BC с заданными данными, так как треугольник невозможно построить.