Дано:
Треугольник ABC и A1B1C1-подобны
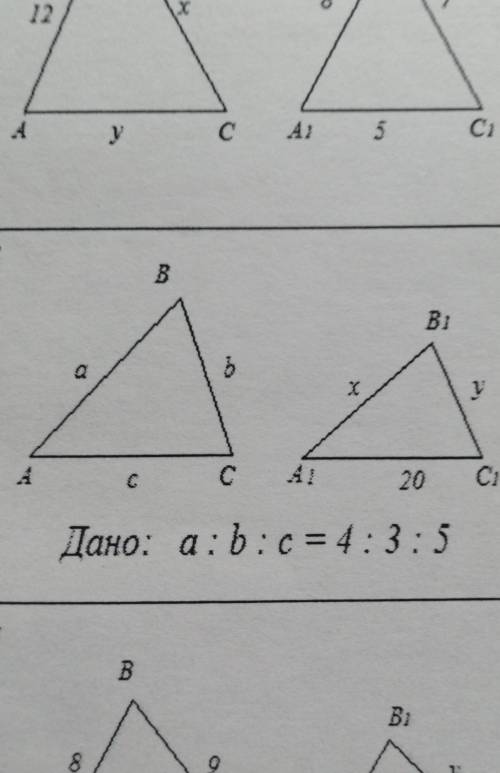
Другие вопросы по теме Геометрия
Популярные вопросы
- 4. Рассчитайте среднесуточную температуру воздуха и амплитуду 3.00 6.00...
1 - 1 2 7 554*, 1) 5 15 29 4 60 7 12 ( 6 7 7 31 14 - 10 24 48 - ( 13 2)...
3 - с алгеброй 2 получил, сказали переделать....
2 - Match 1-8 with A-H to form the compound adjective that means трудоёмкий...
1 - квадрат вписано в коло знайти довжину дуг на які поділяється коло вершинами...
1 - Сколько 9-местых автобусов понадобится для отьезда 84человека на стадионе...
2 - Колонии какой страны раньше располагались преимущественно на востоке...
1 - Деление клетки обеснение биологии...
3 - Назовите животных, которые питаются кормами как растительного, так и...
2 - Користуючись малюнком знайдіть MN × FK...
2
Два треугольника называются подобными, если они имеют равные соответствующие углы и пропорциональные стороны. То есть отношение длин любых двух отрезков, соответствующих сторонам треугольников, одинаково для всех трех пар сторон.
В данной задаче, нам дано два треугольника - треугольник ABC и треугольник A1B1C1. Нам нужно доказать, что они подобны.
Для того, чтобы доказать подобие треугольников ABC и A1B1C1, мы должны убедиться, что углы этих треугольников равны и их стороны пропорциональны.
1. Равенство углов:
Мы видим, что у треугольника ABC есть угол A, угол B и угол C. В треугольнике A1B1C1 также есть угол A1, угол B1 и угол C1. Нам нужно показать, что соответствующие углы равны.
Угол A в ABC соответствует углу A1 в A1B1C1, угол B соответствует углу B1 и угол C соответствует углу C1. Таким образом, углы треугольников ABC и A1B1C1 соответствуют друг другу и, следовательно, они равны.
2. Пропорциональность сторон:
Мы должны проверить, являются ли стороны треугольников ABC и A1B1C1 пропорциональными. Для этого проверим отношение любых двух сторон и убедимся, что оно одинаково для всех трех пар сторон.
Пусть стороны треугольника ABC обозначаются как AB, BC и CA, а стороны треугольника A1B1C1 обозначаются как A1B1, B1C1 и C1A1.
Теперь мы проверим отношение AB/A1B1. Мы замечаем, что AB и A1B1 - это стороны, лежащие на одной прямой, поэтому можно видеть, что отношение их длин составляет AB/A1B1=AB/AE, где E - точка пересечения продолжений сторон AC1 и A1C.
Следуя аналогичной логике, мы можем проверить отношения BC/B1C1 и CA/C1A1. Доказательство подобия треугольников ABC и A1B1C1 завершается, если эти отношения равны.
Общепринятый способ доказательства, который мы можем использовать в этом случае, - это использование принципа подобия треугольников. Если мы докажем, что три пары соответствующих сторон выполняют соотношение равных длин или отношение длин, то треугольники будут подобны.
Во вложенной картинке мы видим, что продолжения сторон ABC пересекаются в точке E, а продолжения сторон A1B1C1 пересекаются в точке E1. Таким образом, мы видим, что оба треугольника ABC и A1B1C1 имеют точку пересечения их продолжений, что является достаточным условием подобия треугольников.
Таким образом, мы можем заключить, что треугольники ABC и A1B1C1 подобны. Это доказывает, что они имеют равные соответствующие углы и пропорциональные стороны.