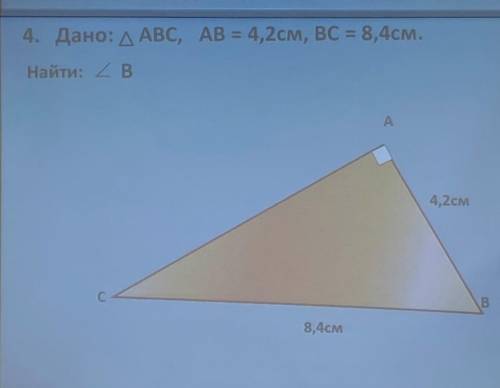
Дано: треугольник abc, AB равно 4,2см , BC равно 8, 4 см .найти угол B.​

60°

Объяснение:

Нам дан прямоугольный треугольник, в котором катет в два раза меньше гипотенузы. По свойству прямоугольного треугольника это означает что ∠С, который находится напротив этого катета, равен 30°.

⇒ ∠В = 180 - 90 - 30 = 60°

Чтобы найти угол B в треугольнике ABC, нам понадобится знание теоремы косинусов. Запишем теорему косинусов для треугольника ABC:

c² = a² + b² - 2ab*cos(C)

где a, b и c - стороны треугольника, C - угол противоположный стороне c.

В нашем случае, a = AB = 4,2 см, b = BC = 8,4 см и c отсутствует.

Так как мы ищем угол B, то нам надо использовать теорему косинусов для нахождения угла B.

c² = a² + b² - 2ab*cos(C)

Сравнивая это с нашими данными, мы видим, что у нас нет информации о угле C.

Однако, у нас есть другая информация — длина сторон треугольника. Мы можем использовать теорему пифагора, чтобы найти недостающую сторону.

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

В нашем случае, длины сторон AB и BC могут быть сторонами прямоугольного треугольника. Используя теорему Пифагора, найдем третью сторону AC.

AC² = AB² + BC²

AC² = (4,2)² + (8,4)²

AC² = 17,64 + 70,56

AC² = 88,2

AC = √88,2

AC ≈ 9,39 см

Теперь у нас есть все три стороны треугольника — AB, BC и AC.

Мы можем использовать теорему косинусов, чтобы найти угол B.

c² = a² + b² - 2ab*cos(C)

AC² = AB² + BC² - 2 * AB * BC * cos(B)

(9,39)² = (4,2)² + (8,4)² - 2 * 4,2 * 8,4 * cos(B)

88,2 = 17,64 + 70,56 - 70,56 * cos(B)

70,56 * cos(B) = 88,2 - 17,64

70,56 * cos(B) = 70,56

cos(B) = 70,56 / 70,56

cos(B) = 1

Теперь, чтобы найти угол, нам необходимо найти арккосинус от значения cos(B):

B = arccos(1)

B = 0 градусов

Итак, угол B в треугольнике ABC равен 0 градусов.