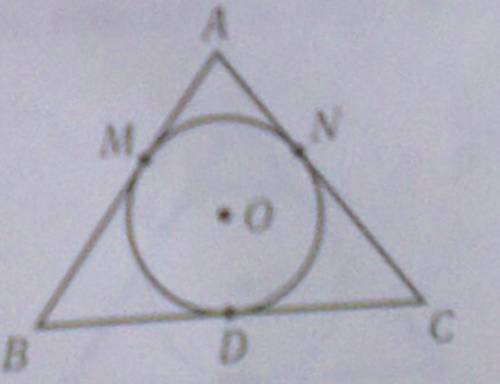
Дано треугольник abc ab=ac=15 см периметр треугольника = 48 см m n d - точки касания сторон и вписанной окружности найдите радиус вписанной окружности (НЕ ИСПОЛЬЗУЯ r=S:p)
Другие вопросы по теме Геометрия
Популярные вопросы
- Ккакой частей речи относятся слова смех смеемся смешно смешинка смешок посмеяться...
1 - Сократите дробь 132132/312312 с решением...
2 - Культура и обычаи бразилии и других стран южной америки ....
1 - Складіть речення із висловом сізіфова праця, ів меч...
2 - Решите уравнения(/-это дроби): 1)x/4=5 2)105/y=7 3)x+12/6=14...
3 - Морфологический разбор числительного, : семьдесят раз в минуту....
2 - Составить 2 с прямой пропорциональностью.(если можно с решением). заранее )...
1 - Какой синоним у слова замерз который начинается...
2 - Составить сказку про экстренные службы: 01 02 03 04...
3 - Составь по уравнения и реши их. 1)если из неизвестного числа вычесть 20, то получиться...
1
r = 4,5
Объяснение:
ВС = 48 - 15 - 15 = 18 см
AD - высота и медиана (т.к. треугольник равнобедренный)
Тогда ΔABD - прямоугольный. АВ = 15, BD = 9
По теореме Пифагора AD = √15² + 9² = √144 = 12
О - точка пересечения биссектрис
ΔODB = ΔOMB т.к.
∠OBD = ∠OBM
OB (гипотенуза) - общая.
Тогда ВМ = 9
АМ = 15 - 9 = 6
По теореме Пиф:
OA² = 6² + r²
OA = √(36 + r²)
AD = 12 = r + OA
r + √(36 + r²) = 12
√(36 + r²) = 12 - r
Возводим обе части в квадрат
36 + r² = 144 - 24r + r²
24r = 144 - 36
24r = 108
r = 4,5