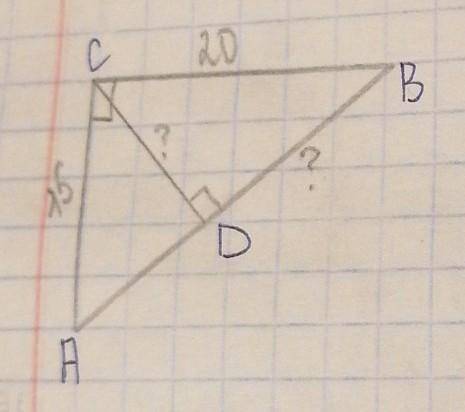
Дано:треуг. ABC - прямоугольный. CD - высота. CB = 20, AC = 15
найти:BD, CD
Другие вопросы по теме Геометрия
Популярные вопросы
- 28 градусов северной широты 88 градусов восточной долготы...
2 - 2. Свяжите процесс работы человека с направлениями предмета информатики....
3 - Изменилось ли ваше первоначальное мнение ? Почему?...
2 - Найдите закономерность 2 3 5 7 11 13 17 ?? ??...
1 - Complete the sentences with the question tags....
2 - 8.3.4. в 40 мл 6%-го раствора нитрата серебра (D [пл. 1,05 г/мл)...
3 - Если к точкам A и B приложить и по ней провести от A к B...
1 - решить, буду премного благодарен вам за это...
1 - 8 класс. Д/З Карточка. Не с различными частями речи. После происшедшего...
1 - 1.17. Чи кожна точка кола належить площині, якщо відомо, що цій...
1
Решение: если АС=15, а СВ=20, то АВ=25 (египетский треугольник).
Найдем высоту СД через площадь ΔАВС. По формуле Герона
S=√(p(p-a)(p-b)(p-c)=√(30*10*15*5)=√22500=150 (ед²).
S=1\2 * AB * CД; 150=1\2 * 25 * СД; СД=150:12,5=12.
Найдем ВД по теореме Пифагора из ΔСДВ:
ВД=√(ВС²-СД²)=√(400-144)=√256=16.
ответ: 12 ед, 16 ед
(если не сложно, то отметьте ответ, как лучший . буду безмерно благодарна!)