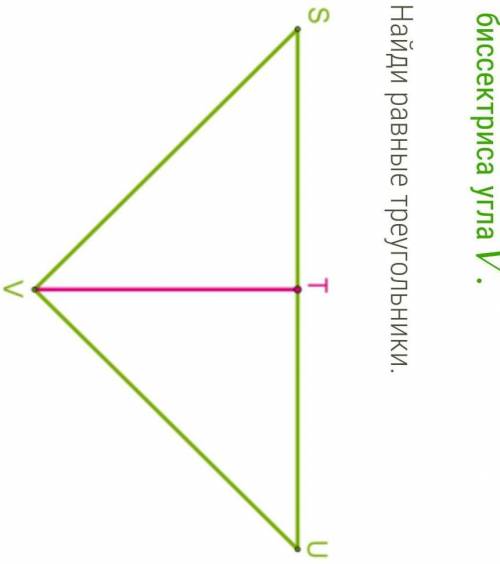
Дано ST VT, TV биссектриса угла V найди равные треугольники (Надо выбрать)
TVU=
1.SVT
2.TVS
3.VST
4.TSV
5.VTS
6.STV

Если известно, что UVT-равнобедренный и прямоугольный, то угол TUV равен

Для решения данной задачи нам необходимо использовать знания о треугольниках, биссектрисах углов и равенстве углов. Дано, что ST VT, TV - биссектриса угла V. Обозначим точку пересечения биссектрисы и стороны ST как точку U. Нам нужно найти равные треугольники, треугольники, в которых все соответствующие стороны и углы равны. Для этого, найдем углы всех возможных треугольников и проверим их равенство. 1) SVT: Угол SVT равен сумме угла VST и угла VTS. Ответ: STV (6) неравны. 2) TVS: Угол TVS равен сумме угла TVU и угла SVU. Ответ: SVT (1) неравны. 3) VST: Угол VST равен сумме угла VTS и угла STV. Ответ: SVT (1) равен. 4) TSV: Угол TSV равен сумме угла TSU и угла USV. Ответ: SVT (1) неравны. 5) VTS: Угол VTS равен сумме угла VST и угла STV. Ответ: SVT (1) равен. 6) STV: Угол STV равен сумме угла SVT и угла VTS. Ответ: SVT (1) равен. Таким образом, из предложенных вариантов, равными треугольниками являются SVT (1), VST (3) и STV (6). Дополнительно дано, что треугольник UVT является равнобедренным и прямоугольным. Равнобедренным треугольником называется треугольник, у которого две стороны равны. Прямоугольным треугольником называется треугольник, у которого один из углов равен 90 градусам. Угол TUV можно найти, используя свойства прямоугольного треугольника. В прямоугольном треугольнике гипотенуза (сторона, противоположная прямому углу) является самой длинной стороной, а катеты (стороны, прилегающие к прямому углу) являются более короткими сторонами. В данном случае, стороной UVT, является гипотенуза. Найдем угол TUV по теореме Пифагора: VT^2 = ST^2 + SV^2 VT^2 - ST^2 = SV^2 SV = sqrt(VT^2 - ST^2) Теперь, используя свойства прямоугольных треугольников, найдем угол TUV: sin(TUV) = ST / VT TUV = arcsin(ST / VT) Таким образом, чтобы найти значение угла TUV, необходимо знать значения сторон ST и VT, и подставить их в формулу. Изначально, на данной фотографии отсутствуют значения длин сторон ST и VT. Если известны эти значения, их можно использовать для нахождения угла TUV.