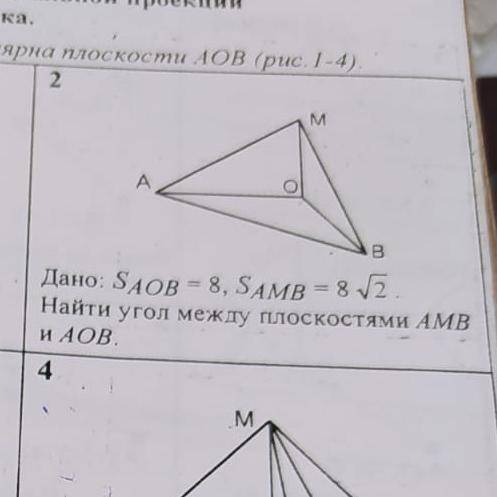
Дано Saob=8, Samb=8корень из 2,найдите угол между плоскостями AMB и AOB
Другие вопросы по теме Геометрия
Популярные вопросы
- Нужна . если можно, то напишите подробное решение 1. рассчитайте количество...
3 - Апрямоугольном тоеугольникн косинус угла между гипотегузой и катетом...
1 - Переделать в разговорную речь -пап, а можно я не буду есть этот суп?...
1 - Ибольше общий делитель числа 680 и 612...
3 - Сочинить самим не большое стихотворение про знаки препинания...
1 - C3h8-c3h7cl-c3h7oh-c3h6-co2 решите уровнение реакции...
2 - Составить диалог со словами құрмет,сыпайлық, əдеп,апарысу,тəрбие,белгі,үлгі,...
3 - Чем похож илья муромец на персонажей героического эпоса других народов?...
2 - Уважаемые люди такой вопрос в чём заелючается нравственность ивана царевича...
1 - Пример: 16*25=4*(4*25)=4*100=400 75*12 75*44 нужно решить эти 2 примера...
2
Направляющие векторы плоскостей AMB и AOB можно найти с помощью скалярного произведения нормального вектора плоскости и некоторого другого вектора на плоскости.
1. Найдем направляющий вектор плоскости AMB:
У нас дано Samb = 8√2. Так как плоскость AMB проходит через точки A, M и B, мы можем использовать точки M и B для нахождения направляющего вектора плоскости AMB. Найдем вектор MB, который является разностью координат векторов M и B:
MB = [xM - xB, yM - yB, zM - zB]
2. Теперь найдем направляющий вектор плоскости AOB:
У нас дано Saob = 8. Плоскость AOB проходит через точки A, O и B, поэтому используем точки O и B для нахождения направляющего вектора плоскости AOB. Найдем вектор OB, который является разностью координат векторов O и B:
OB = [xO - xB, yO - yB, zO - zB]
3. Найдем нормальные векторы плоскостей AMB и AOB:
Нормальный вектор плоскости представляет собой вектор, перпендикулярный плоскости. Для этого воспользуемся векторным произведением направляющих векторов плоскостей AMB и AOB:
нормальный вектор плоскости AMB = MB x AB
нормальный вектор плоскости AOB = OB x AB
4. Используем скалярное произведение нормальных векторов и формулу cos угла между векторами для нахождения угла между плоскостями AMB и AOB:
cos(угла между плоскостями AMB и AOB) = (нормальный вектор плоскости AMB * нормальный вектор плоскости AOB) / (длина вектора нормального вектора плоскости AMB * длина вектора нормального вектора плоскости AOB)
Разберем подробнее каждый из шагов для данной конкретной задачи:
1. Найдем вектор MB:
MB = [xM - xB, yM - yB, zM - zB]
MB = [1 - (-√2), 2 - 0, 0 - 1]
MB = [1 + √2, 2, -1]
2. Найдем вектор OB:
OB = [xO - xB, yO - yB, zO - zB]
OB = [0 - (-√2), 0 - 0, 1 - 1]
OB = [√2, 0, 0]
3. Найдем нормальный вектор плоскости AMB:
нормальный вектор плоскости AMB = MB x AB
AB = (1, 0, 1) - (1, 0, 0) = (0, 0, 1)
нормальный вектор плоскости AMB = [2, 1 + √2, 0 - (1 + √2)]
нормальный вектор плоскости AMB = [2, -√2, -1 - √2]
4. Найдем нормальный вектор плоскости AOB:
нормальный вектор плоскости AOB = OB x AB
нормальный вектор плоскости AOB = [√2, 0, 0] x [0, 0, 1]
нормальный вектор плоскости AOB = [0, -√2, 0 - 0]
нормальный вектор плоскости AOB = [0, -√2, 0]
5. Рассчитаем длины нормальных векторов плоскостей AMB и AOB:
длина вектора нормального вектора плоскости AMB = √(2^2 + (-√2)^2 + (-1 - √2)^2)
длина вектора нормального вектора плоскости AMB = √(4 + 2 + 1 + 2√2 + 2√2 + 2)
длина вектора нормального вектора плоскости AMB = √(9 + 4√2 + 2)
длина вектора нормального вектора плоскости AMB = √(11 + 4√2)
длина вектора нормального вектора плоскости AOB = √(0^2 + (-√2)^2 + 0^2)
длина вектора нормального вектора плоскости AOB = √(2)
длина вектора нормального вектора плоскости AOB = √2
6. Найдем скалярное произведение нормальных векторов плоскостей AMB и AOB:
(нормальный вектор плоскости AMB * нормальный вектор плоскости AOB) = (2 * 0) + (-√2 * -√2) + (-1 - √2 * 0)
(нормальный вектор плоскости AMB * нормальный вектор плоскости AOB) = 2 + 2 + 0
(нормальный вектор плоскости AMB * нормальный вектор плоскости AOB) = 4
7. Найдем косинус угла между плоскостями AMB и AOB:
cos(угла между плоскостями AMB и AOB) = (4) / (√(11 + 4√2) * √2)
cos(угла между плоскостями AMB и AOB) = (4) / (√2 * √(11 + 4√2))
cos(угла между плоскостями AMB и AOB) = (4) / (√(2 * (11 + 4√2)))
cos(угла между плоскостями AMB и AOB) = (4) / (√(22 + 8√2))
Таким образом, угол между плоскостями AMB и AOB можно найти, найдя косинус этого угла. В данном случае косинус угла между плоскостями AMB и AOB равен (4) / (√(22 + 8√2)).