Дано:ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК MNK. NK-X
MN-Y
NP-ВЫСОТА, МЕДИАНА. 6 СМ
MP-z
PK-12
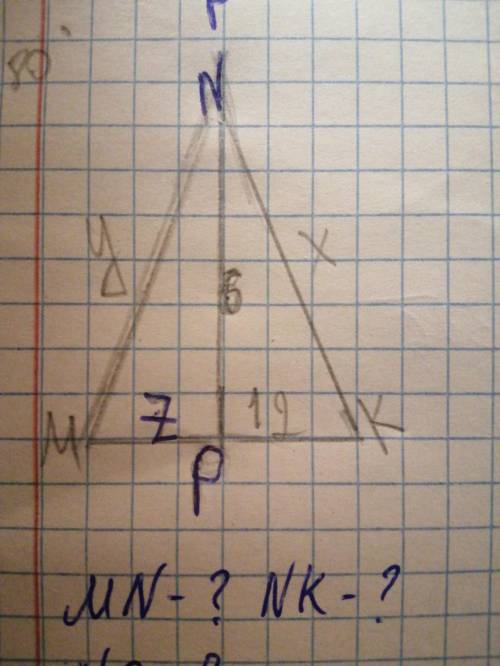
Другие вопросы по теме Геометрия
Популярные вопросы
- 9,6 ц = ? кг поставьте ответ на место вопроса....
1 - Написать аннотацию на тему лес зимой...
3 - Какие есть изобретения древних китайцев 5 класс....
3 - Условие : миша,ваня и коля купили лотерейный билет. миша внёс 12...
3 - Найдите одно коренные слова и запишите их в пары хлеб дуб хлебный...
1 - Составте сочинение по теме муму по плану : 1) мое отношение к герасиму....
1 - Преобразуйте в многочлен выражение. 1) (x+y)(2x-y)(3x+y) 2) (x^2-3x+1)(x^2+3x+1)...
1 - Определить композицию и размер стиха н.заболоцкого летний вечер...
1 - Эссе на тему: должна быть экономной. брежнев . с доказательствами...
2 - Укажите, какое значение соответствует следующим образным выражениям....
1
Дано:
- В треугольнике МНК, стороны МН и МК образуют прямой угол.
- На стороне МН имеется точка X, на стороне МК – точка Y.
- Сторона NК - высота и медиана.
- Длина медианы – 6 см.
- Длина стороны МР обозначена буквой z и неизвестна.
- Длина стороны РК равна 12 см.
Чтобы найти длину стороны МP, мы можем воспользоваться теоремой Пифагора. Согласно этой теореме, квадрат гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов катетов (двух оставшихся сторон).
Итак, применяем теорему Пифагора к треугольнику МRK:
МР² = МП² + РК².
Известно, что РК = 12 см, заменяем данное значение в уравнение:
МР² = МП² + 12².
Теперь обращаемся к дополнительному треугольнику МНP. Дано, что сторона NP является высотой и медианой треугольника МНК. Известно, что длина медианы равна 6 см. В треугольниках высота, проведенная к гипотенузе, делит ее на две равные части.
Таким образом, МП = NP = 6 см.
Заменяем МП на 6 в уравнение:
МР² = 6² + 12².
МР² = 36 + 144.
МР² = 180.
Теперь извлекаем квадратный корень из обеих сторон уравнения:
МР = √180.
МР = √(36 ⋅ 5).
МР = √36 ⋅ √5.
МР = 6√5.
Таким образом, длина стороны МP равна 6√5 см.
Надеюсь, это ответ четко объясняет, как был получен результат. Если остались вопросы, не стесняйтесь задавать их!