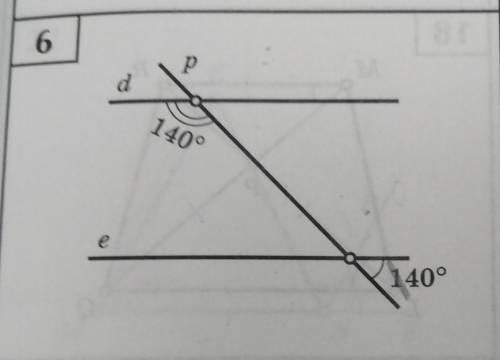
Дано прямая d, p, e. Прямая р пересекает d и е, образовывая углы 140 градусов и 40 градусов. Докажите, что прямые d и e параллельны. ​

Для доказательства, что прямые d и e параллельны, мы можем использовать свойства параллельных прямых и аксиому, которая говорит, что сумма углов треугольника равна 180 градусов.

Итак, давайте рассмотрим данный нам угол 140 градусов. Из аксиомы о сумме углов треугольника мы знаем, что сумма углов треугольника равна 180 градусам. Поэтому мы можем вычислить второй угол треугольника п.

180 градусов - 140 градусов = 40 градусов

Теперь мы видим, что второй угол треугольника п равен 40 градусам.

Следующий шаг - рассмотреть углы, образованные прямой р с прямыми д и е. Мы знаем, что сумма углов треугольника равна 180 градусам. Поэтому, чтобы найти меру угла, образованного прямой р и прямой д, мы должны вычесть от 180 градусов известные нам углы.

180 градусов - 140 градусов = 40 градусов

Мы видим, что угол между прямыми р и д также равен 40 градусам.

Теперь давайте рассмотрим угол, образованный прямой р и прямой е. Известно, что сумма углов треугольника равна 180 градусам. Поэтому, чтобы найти меру угла, образованного прямой р и прямой е, мы также должны вычесть от 180 градусов известные нам углы.

180 градусов - 40 градусов = 140 градусов

Мы видим, что угол между прямыми р и е также равен 140 градусам.

Итак, мы получили, что уголи между прямой р и прямыми д и е равны и 40 градусам, и 140 градусам.

Теперь важно заметить, что угол между параллельными прямыми соответствующий (имеющий одинаковую меру) и составляющий альтернативные внутренние углы параллельных линий, одновременно равен каждому из этих углов. В нашем случае, один из углов равен 40 градусам, а другой - 140 градусам.

Поэтому, согласно этому свойству, мы можем заключить, что прямые д и е являются параллельными. Они имеют параллельные прямые р, которые пересекают их, образуя углы равные 140 градусам и 40 градусам.

Таким образом, мы доказали, что прямые d и e параллельны.

дано оавзузцрцрцоа
₽:&373(
Шщунйоудудалгуоц
Улркоуллулц