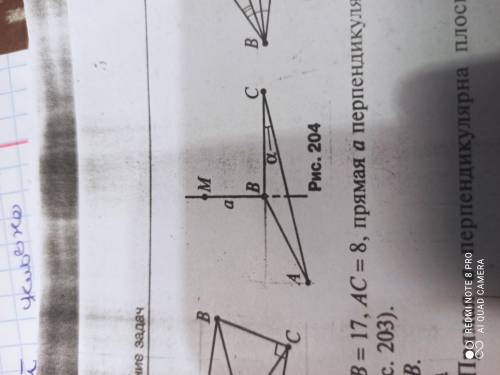
Дано: Прямая а перпендикулярна плоскости (АВС) (рис. 204) Найти: Расстояние от точки М до прямой АС.
ответ: 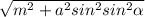
Другие вопросы по теме Геометрия
Популярные вопросы
- ответьте на во Какие темы затрагивают песни о Великой Отечественной войне?...
1 - Установите соответствие между представителями и их передвижения А аполлон Б сазан...
1 - Найдите диаметр сферы если её площадь равна 1*25\63...
3 - 2. Юшка считал, что дети его любят, но так как любить они не умеют, то и терзают...
2 - ну где вы говорпили Выполните заданиеСреди предложений 17–21 найдите предложение...
3 - -1/4*|х Х1-Х2-Первым запмши наименьшее число...
1 - В треугольнике САВ отметь сторону, противолижащию углу АСВ...
2 - Давньоримські дорогі. Які дорогі вони строїли і їх опис Дам 35 Б. ОЧЕНЬ...
2 - Тест «Правописание окончаний и суффиксов имен существительных» 1. В каком слове...
1 - Укажи сопряжение глаголов :мыть. светят .гонят. стелют (постель).покупаешь.рубил...
1
Дано:
Прямая а перпендикулярна плоскости (АВС) и имеет точку М.
Плоскость (АВС) образует треугольник АВС.
Найти:
Расстояние от точки М до прямой АС.
Решение:
1. Определим основные данные и обозначения в задаче:
- m: расстояние от точки М до прямой АС (используется в ответе)
- a: расстояние от точки М до перпендикуляра а (используется в ответе)
- α: угол, образованный перпендикулярной линией а и прямой АС
2. Вспомним теорему Пифагора:
В прямоугольном треугольнике гипотенуза в квадрате равна сумме квадратов катетов.
У нас есть прямоугольный треугольник, образованный гипотенузой АС и катетами а и МС.
3. Запишем теорему Пифагора для этого треугольника:
МС² = а² + МА²
4. Поскольку нас интересует расстояние от точки М до прямой АС, то МС характеризует это расстояние, поэтому обозначим его как m.
Теперь наше уравнение будет иметь вид:
m² = а² + МА²
5. Согласно рисунку, угол α образован перпендикуляром а и прямой АС.
Так как у нас имеется перпендикуляр, то угол α является прямым углом (90 градусов).
6. Вместо МА в уравнение Пифагора подставим а*sin(α), что представляет собой катет прямоугольного треугольника:
m² = а² + (а*sin(α))²
7. По теореме Пифагора, решим уравнение:
m² = а² + (а*sin(α))²
m² = а² + а²*sin²(α)
8. Упростим уравнение:
m² = а² * (1 + sin²(α))
9. Таким образом, расстояние от точки М до прямой АС равно корню из величины а²*(1+sin²(α)).
Ответ можно записать как:
Расстояние от точки М до прямой АС = √(а²*(1+sin²(α)))
Это и есть окончательный ответ.