Дано: Pabc = 40. Найти: Pa1b1c1.
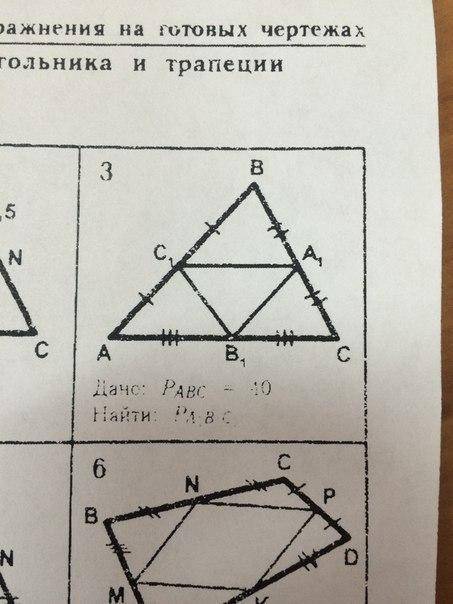
Другие вопросы по теме Геометрия
Популярные вопросы
- Дайте відповідь на 4,5,6....
2 - Проведите небольшое иследование предложи своим близким друзьям определить...
1 - Алые паруса 1.место действие произведения2. Отношение жителей к Ассоль и...
1 - Угол akm равен углу kac. найдите значение выражения1/4(угол bac + угол amk)...
3 - Надеюсь все видно Очень нужно люди на завтра тчень нужно людии НЕ ПИШИТЕ...
2 - Поясніть чинники розміщення трьох центрів виробництва окремих транспортних...
2 - Буду очень благодарен, 5 4/14 + 3 9/14 =...
2 - Напишите уравнение реакции гидролиза для гидролиза солей K2S, K2SO4, K2So3...
1 - не писать ерунду, буду кидать жалобу)...
3 - Извиняюсь за спам вопросами, но если я отправлю весь тест (18 вопросов)...
2
Зная, что Pabc = 40, мы можем записать следующее равенство:
Pabc = Pa * Pb * Pc
Теперь давайте найдем значение Pa, Pb и Pc из заданной информации.
Из рисунка видно, что Pa равно 9. То есть, Pa = 9.
Теперь рассмотрим значение Pb. На рисунке видно, что отсутствует информация о вероятности Pb иначе, как только сравнение. Зная, что Pa=9, мы можем сделать предположение, что Pb тоже равно 9 (так как это единственный коэффициент, с которым мы можем сравнить значние Pa). Однако, это лишь предположение и не дано достаточного количества информации для точного определения значения Pb.
Теперь рассмотрим значение Pc. На рисунке видно, что Pc равно 10. То есть, Pc = 10.
Итак, у нас есть следующие значения:
Pa = 9
Pb = неизвестно
Pc = 10
Теперь используем найденные значения для вычисления Pa1b1c1.
Pa1b1c1 = Pa1 * Pb1 * Pc1
Здесь мы предполагаем, что индексы 1 обозначают новые значения, которые мы ищем.
Теперь у нас есть две задачи: найти значение Pb1 и Pa1.
Для нахождения Pb1, мы можем использовать отношение вероятностей. Мы знаем, что Pb равно некоторому значению, и нам нужно найти Pb1 относительно этого значения. Таким образом, мы можем записать следующее равенство:
Pb / Pb = Pb1
Если мы делим что-то на себя, мы получаем единицу, поэтому Pb1 = 1.
Теперь у нас остается только найти значение Pa1. Мы можем использовать отношение вероятностей, поскольку у нас есть некоторые значения, связанные между собой. Мы знаем, что Pa равно 9, и нам нужно найти Pa1 относительно этого значения. Таким образом, мы можем записать следующее равенство:
Pa / 9 = Pa1
Для нахождения Pa1 можно поделить обе части равенства на 9:
Pa1 = Pa / 9 = 9 / 9 = 1.
Таким образом, мы получаем следующие значения:
Pa1 = 1
Pb1 = 1
Pc1 = 10
Итак, Pa1b1c1 = 1 * 1 * 10 = 10.
Ответ: Pa1b1c1 = 10.