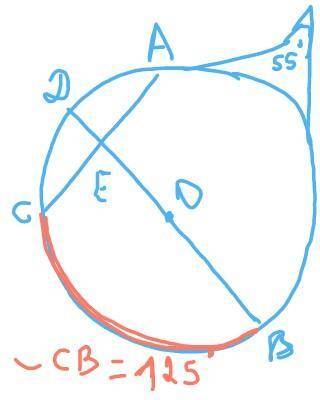
Дано, PA и PB касательные, BD диаметр. угол APB= 55° градусов, дуга CB = 125°. Найдите дугу AB, угол DEC дугу AD, угол PBD, угол PAC . В левой верхней части там угол P
Другие вопросы по теме Геометрия
Популярные вопросы
- 4sin(квадрат)15(градусов)*соs(квадрат)15(градусов) нужно решить...
2 - Вмолекуле днк количество нуклеотидов с гуанином составляет 30 от общего числа.какой...
2 - Ниже перечень терминов. все они,за исключением одного,относятся к событиям явления...
2 - 21 ноября мы узнали от наших тыловых частей, которые располагались на восточном...
2 - Вкаком из случаев вступает в действие закон рф о защите прав потребителей? 1) склад...
3 - Квнутриним функциям государства что относиться?...
1 - Что являеться причиной социальных конфликтов?...
3 - Какой гормон и с какой целью больным сахарным диабетом? почему его вводят внутривенно,...
2 - 1-какая из перечисленных столиц европейских государств была освобождена от фашистов...
3 - Что является вегетативным органом цветкового растения ? ?...
3
Дано, PA и PB касательные, BD диаметр, ∠APB= 55°, дуга ∪CB = 125°. Найдите дугу ∪AB, ∠ DEC , дугу ∪AD, ∠PBD, ∠PAC .
Объяснение:
1) Сумма углов четырехугольника АОВР равна 360°.Тк РА и РВ касательные , то ∠ОАР=∠ОВР=90° ⇒ ∠АОВ=360°-2*90°-55°=125°
По свойству центрального угла ∠АОВ=∪АВ=125° .
2)∠ДЕС=(∪АВ+∪СД):2 по свойству угла, образованного пересекающимися хордами.
ДВ-диаметр ⇒ ∪ВД=180° ⇒ ∪СД=180°-125°=55° , ∠ДЕС=(125°+55°):2=90°.
3) ∠РВД=90° , тк РВ-касательная.
4) ∠РАС=∠РАО+∠АОД
∠АОД=180-∠АОВ по т о смежных углах, ∠АОД=55°.
∠РАС=90°+55°=145°.
Свойство угла , образованного пересекающимися хордами : "Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами."