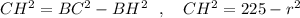Дано:
Окружность с центром О, треугольник АВС вписанный в эту окружность, касательная к окружности ВН
АВ=20, ВС=15,
ВН перпендикулярна АС
Найти АС
За спам минус и бан, как обычно.
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите главную мысль текста. богатства языка не измеримы. они прото...
3 - Решение 37800: 700=? скажите как решить и сами мне напишите надо...
2 - Пож написать на достопримечательности лондона по 2-3 предложения на...
1 - Яучусь в 6 классе и мы по проходим всякие радиусы окружности , шары...
3 - Из со сжатым водородом емкостью 10л вследствие неисправности вентиля...
3 - 1) с какими из перечисленных веществ будет реагировать цинк гидроксид:...
1 - Составить словосочетание со словом: мою-ударение на о,мою-ударение...
3 - Решить : из поселка вышли одновременно в противоположных направлениях...
1 - Установите соответствие между характеристикой процесса и деления клетки,...
2 - Описание игнатьича в капитанской дочке...
1
ответ: AC=7 .
Объяснение:
Обозначим α=∠ВАС , он опирается на дугу ВС, значит равен половине угловой величины дуги ВС.
Угол между касательной ВН и хордой ВС равен половине угловой величины дуги, заключенной между ними.,то есть дуги ВС .
Значит, ∠ВАС=∠СВН .
Отрезок ВН равен радиусу окружности: r=BH .
Из ΔАВН: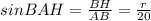 .
.
Из ΔВСН: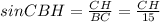 .
.
Из ΔАВН: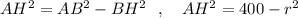
Из ΔВСН: