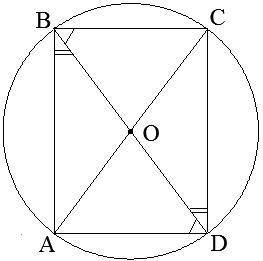
Дано: окружность с центром O и радиусом DO. Равны ли треугольники AODиAOB по второму признаку равенства треугольников? ΔAOD=ΔAOB?

Не равны

Равны

Чтобы определить, равны ли треугольники AOD и AOB по второму признаку равенства треугольников, нужно сравнить их стороны и углы.

По определению, второй признак равенства треугольников гласит, что два треугольника равны, если две их стороны и угол между ними равны.

Первым шагом рассмотрим стороны треугольников AOD и AOB. Мы видим, что сторона AO у обоих треугольников имеет одинаковую длину, так как это радиус окружности. Также сторона OD или OB имеют одинаковую длину, так как это радиусы дуг AD и AB соответственно. Таким образом, мы можем сказать, что стороны AO и OD (или OB) равны.

Вторым шагом рассмотрим углы треугольников. Мы знаем, что центральный угол AOD равен центральному углу AOB, так как они стягивают дуги AD и AB соответственно. По определению, центральные углы, стягивающие одинаковые дуги, равны. Таким образом, мы можем сказать, что угол AOD и угол AOB равны.

Итак, мы установили, что стороны AO и OD (OB) равны, а также угол AOD и угол AOB равны. Следовательно, треугольники AOD и AOB равны по второму признаку равенства треугольников.

Ответ: Равны.