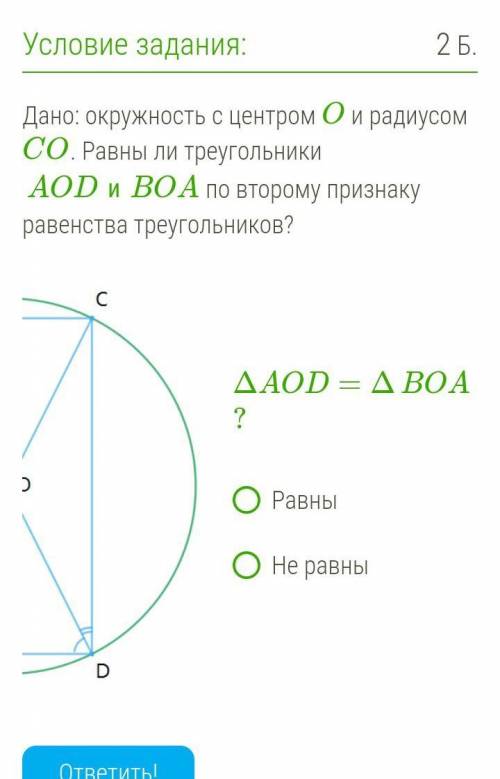
Дано: окружность с центром O и радиусом CO. Равны ли треугольники AODиBOA по второму признаку равенства треугольников? ΔAOD=ΔBOA? Равны Не равны
Другие вопросы по теме Геометрия
Популярные вопросы
- Господи, Решите все задачи. 9 класс. ...
3 - деление с остатком (в виде столбика) ну ...
1 - Координаталық жазықтықта АВСD тік төртбұрышының А(-2;-2), В(-2;2) және...
3 - это 1.Выпиши из предложений местоимения (без предлогов). Укажи, какие...
1 - Талгат Амангелдиевич Мусабаев (род. 7 января 1951 г.). Народный Герой...
3 - у водах Тихого океана проплыл корабль прибывает в каких морях и Затока...
3 - 6.5 тон переводите в систему си (кг) -...
1 - Частоты групп крови по системе ABO в некоторой популяции человека следующие:...
3 - Прочитайте и определите в тексте слова с ошибками, расставьте знаки...
2 - вы задумывались об этом? лично я, всегда._....
2
Второй признак равенства треугольников гласит: Если два треугольника имеют равные стороны, расположенные между равными углами, то эти треугольники равны.
На рисунке дано, что треугольник AOD является равнобедренным, так как OA=OD (радиус окружности).
Теперь нужно сравнить треугольник BOA с треугольником AOD по второму признаку равенства треугольников.
Стороны, расположенные между равными углами в треугольнике AOD: AD и DO.
Требуется проверить, равны ли эти стороны соответствующим сторонам треугольника BOA.
Так как сторона AD треугольника AOD соответствует стороне OA треугольника BOA (они равны, так как это радиусы одной и той же окружности), они равны.
Также сторона DO треугольника AOD соответствует стороне AB треугольника BOA (они равны, так как это радиусы одной и той же окружности), они также равны.
Таким образом, треугольники AOD и BOA имеют равные стороны, расположенные между равными углами, поэтому они равны по второму признаку равенства треугольников.