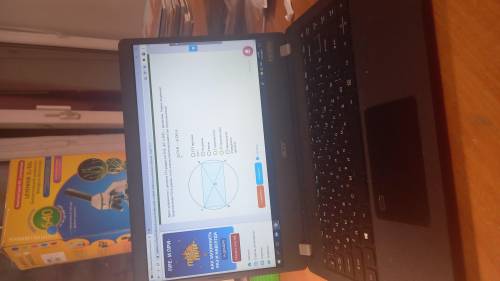
Дано: окружность с центром о и радиусом АО. АС и BD - диаметры. Равны ли данные треугольники? Если равны то по какому признаку равенства треугольников?
Другие вопросы по теме Геометрия
Популярные вопросы
- Заполни таблицу, вписав в неё слова с буквосочетанием -оро- (в одну клетку вписывай...
1 - Зарание ) 1) какую роль сыграл советский союз в освобождении стран восточной...
3 - Тригонометрическое выражение: sin ( 35пи/2 -альфа) + cos ( 68 пи - альфа)...
1 - Площадь первого участка 120 м в квадрате, второго 160 м в квадрате. при одинаковой...
2 - Разделите слово библиотеку по слогам....
1 - Прочитала 25 страниц.утром5 страниц, днем 8 страниц. сколько вечером.надо разные...
3 - Знайдіть площу паралелограма, у якого діагоналі дорівнюють 8 см і 10 см, а кут...
3 - Составить рецепт любого блюда, употребляя изъявительное наклонение....
2 - Запишите символы металлов, окисление которых кислородом на воздухе невозможно:...
1 - Пассажирский поезд путь от одной станции до другой со средней скоростью 67км/ч....
3
На данной картинке изображена окружность с центром O и радиусом АО. Также дано, что АС и BD - диаметры окружности.
Давайте обратимся к определению равенства треугольников. Два треугольника считаются равными, если у них равны соответствующие стороны и равны соответствующие углы.
Исходя из этого определения, чтобы убедиться в равенстве треугольников, нужно проверить равенство их сторон и углов.
Начнем с равенства сторон. Мы видим, что сторона АС является диаметром окружности, а сторона АО - радиусом. Так как диаметр в два раза больше радиуса, можно сделать вывод, что АС = 2 * АО.
Аналогично, сторона BD также является диаметром окружности, поэтому BD = 2 * АО. Таким образом, стороны треугольников АСО и ВDO равны между собой.
Теперь давайте проверим равенство углов. В данном случае мы видим, что треугольник АСО является прямоугольным, так как его сторона АО является радиусом окружности, а сторона АС - диаметром, которые всегда перпендикулярны на окружности. Аналогичная ситуация и у треугольника BDO. Поэтому, углы треугольников АСО и BDO равны между собой.
Таким образом, мы получаем, что треугольники АСО и BDO равны между собой по признаку равенства сторон и углов.
В итоге, ответ на данный вопрос: треугольники АСО и BDO равны между собой.