Дано np=2rn и rm: mq=1: 8. найдите нужные отношения. pk: pq ks: sr pl: ls

Ответы

Darina1110 02.10.2020 00:10

Такую задачу можно делать с теоремы о пропорциональных отрезках, но при этом нужно проводить дополнительные линии, а мне делать это лень. Поэтому воспользуемся теоремой Менелая. Советую перед разбором решения ознакомиться с формулировкой этой теоремы. А заодно и с теоремой Чевы. А если посмотрите и теорему Ван-Обеля, вы будете подкованы на 100%.

Кстати, удобно сначала воспользоваться теоремой Чевы. Поскольку чевианы PM, RK и QN пересекаются в одной точке, справедливо равенство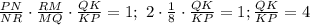 $\frac{PN}{NR}\cdot \frac{RM}{MQ}\cdot \frac{QK}{KP}=1;\ 2\cdot \frac{1}{8}\cdot \frac{QK}{KP}=1; \frac{QK}{KP}=4$ .

То есть в QK четыре части, а в KP одна часть. Следовательно, в PQ=PK+KQ пять частей, а тогда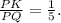 $\frac{PK}{PQ}=\frac{1}{5}.$

Для нахождения второго отношения воспользуемся теоремой Ван-Обеля. Поскольку чевианы PM, RK и QN пересекаются в точке S, то

$\frac{RS}{SK}=\frac{RN}{NP}+\frac{BM}{MQ}=\frac{1}{2}+\frac{1}{8}=\frac{5}{8}\Rightarrow \frac{KS}{SR}=\frac{8}{5}$

Для нахождения третьего отношения применим теорему Менелая к треугольнику PRS и прямой NK, которая пересекает стороны PR и PS и продолжение стороны RS. Имеем:

$\frac{PL}{LS}\cdot \frac{SK}{KR}\cdot \frac{RN}{NP}=1;$ $\frac{PL}{LS}\cdot \frac{8}{13}\cdot \frac{1}{2}=1;$

$\frac{PL}{LS}=\frac{13}{4}$

Внимание для тех, кто хочет (и знает, как) сделать сайт лучше и комфортнее! В данный момент я имею в виду не преодоление тех очевидных недостатков, которые становятся очевидными в первые пять минут, а плохую работу встроенного TEX'а. Впечатление, что здешние айтишники не знают, как решить возникающие проблемы. Предложите им свои услуги!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия