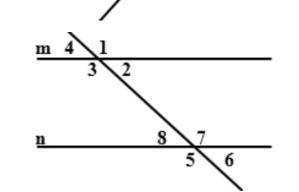
Дано:m || n
<2 + <8 = 100°
Найти: остальные углы

Для решения данной задачи, нам понадобится знание о параллельных прямых и о сумме углов треугольника.

Итак, у нас есть две параллельные прямые m и n, и в точке их пересечения есть угол <2. Также, одна из параллельных прямых пересекает третью прямую, образуя угол <8.

Используя свойство параллельных прямых, мы можем сказать, что <2 и <8 являются корреспондирующими углами (это означает, что они находятся на одной стороне от пересекающей прямой и между параллельными прямыми), и они равны.

А также, вся сумма углов треугольника равна 180°. Мы знаем, что <2 + <8 = 100°. Нам нужно найти остальные углы треугольника.

Найдем угол <4. У нас есть две параллельные прямые, поэтому две пары углов, корреспондирующие углы, будут равны. То есть, <2 = <4. Поэтому у нас есть <4 = <2 = 100°.

Теперь мы можем найти угол <1. Сумма всех углов треугольника равна 180°, и мы уже знаем, что <2 = 100° и <4 = 100°. Подставим это в уравнение:
<1 + <2 + <4 = 180°
<1 + 100° + 100° = 180°
<1 + 200° = 180°
<1 = 180° - 200°
<1 = -20°

Таким образом, мы нашли, что угол <1 равен -20°. Это может показаться странным, потому что углы не могут быть отрицательными. Но это говорит о том, что наша исходная информация должна быть неправильной или противоречивой. Возможно, мы сделали ошибку в измерении углов или приняли неверные данные.

В любом случае, нам необходимо пересмотреть исходные данные и переделать решение. Если задача предполагает правильные исходные данные и решение, то, вероятно, там есть ошибка или опечатка.

Надеюсь, что это объяснение поможет вам лучше понять процесс решения такой задачи! Если у вас есть еще вопросы, пожалуйста, дайте знать.