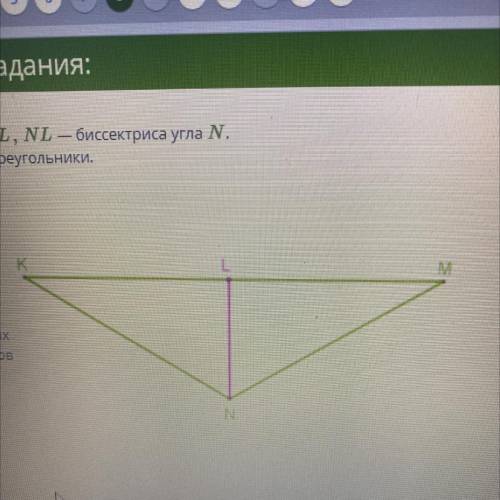
Дано: KL l NL, NL — биссектриса угла N. Найди равные треугольники,
LNK =
O MNL
OLMN
ONML
Онет равных
треугольников
ONLM
MLN
O LNM
Другие вопросы по теме Геометрия
Популярные вопросы
- Написать рассуждение на тему если бы земля не притягивала...
3 - Почему у рыб, мечущих икру на быстром течении, икра клейкая и тяжелая,...
1 - 15-8=9 а+30=30+а 11-у=7 х-х=0 с+3=12 14 25-20=5 14+е=е n+20=42 синем карандашом...
2 - Вкаком из этих стихотворных отрывков слово проволока произносится несколько...
3 - Как проверить первую е в слове температура?...
2 - Можно ли утверждать,что в обычной клетке идут все процессы,характерные...
3 - Впрямоугольнике авс угол с- прямой, внешний угол вак=120°, ав+ас=36. найдите...
3 - Возраст ивана ивановича 48 лет 48 месяцев 48 недель 48 дней 48 часов....
2 - Ядро это литосфера гидросфера биосфера или атмосфера. манти я это литосфера...
2 - Витя попросил папу купить ему три машинки: красную,зелёную и синюю. папа...
1
1) KL || NL - это означает, что отрезки KL и NL параллельны друг другу.
2) NL - биссектриса угла N - это означает, что угол KNL равен углу LNL. То есть угол KNL = угол LNL.
3) KL и NL пересекаются в точке N.
Теперь рассмотрим предложенные треугольники:
LNK:
Угол KNL = угол LNL (так как NL - биссектриса угла N).
Угол K и угол L соответственно равны углам M и N (по свойству параллельных прямых).
О МNL:
Угол KNL = угол LNL (так как NL - биссектриса угла N).
Угол L и угол M соответственно равны углам K и N (по свойству параллельных прямых).
OLMN:
Угол KNL = угол LNL (так как NL - биссектриса угла N).
Угол M и угол L соответственно равны углам N и K (по свойству параллельных прямых).
ONML:
Угол KNL = угол LNL (так как NL - биссектриса угла N).
Угол N и угол M соответственно равны углам L и K (по свойству параллельных прямых).
Из данных и свойств можно сделать следующие выводы:
- Треугольник LNK равен треугольнику O MNL, так как имеют равные углы и одну равную сторону NL (в качестве общей стороны).
- Треугольник LNK равен треугольнику OLMN, так как имеют равные углы и одну общую сторону LN (в качестве общей стороны).
- Треугольник LNK равен треугольнику ONML, так как имеют равные углы и одну общую сторону LN (в качестве общей стороны).
- Треугольник LNK не равен треугольнику ONLM, так как они имеют одну общую сторону LN, но не имеют равных углов.
- Треугольники ONLM, MLN и O LNM не могут быть рассмотрены как равные треугольники, так как не имеют равных углов и равных сторон.
Таким образом, равные треугольники в данной задаче - LNK равен O MNL равен OLMN равен ONML. Остальные треугольники не являются равными.