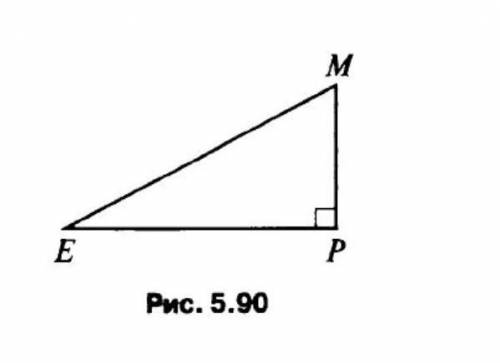
Дано: ∠EPM = 90°, ∠MEP = 30°, ME = 10 см (рис. 5.90).РМ нужно
Другие вопросы по теме Геометрия
Популярные вопросы
- Как разделить счисло 432 на 9 в столбик ! 1...
1 - Определите время я якутске и в магадане . если в астане 12 часов...
3 - Кто является автором принципа разделения власти: а) дж. локк б) ш. монтескье...
3 - Устройства которое регулировать движение...
2 - Мағжан жұмабаевтің пайғамбар өлеңі керек еді...
3 - Объясните как решать степенную функцию y=x^6...
1 - Каждой девочке - веселушки соответствует однозначное число...
1 - Может быть два суффикса в одном слове?...
2 - Умоего друга мягкий характер. какое значение прямое или переносное...
2 - Из числа 13 вычти разность чисел 11 и 8 . к сумме чисел 8 и 6 прибавь число...
2
Из условия, что один из углов прямой а их всего 3 следует, что это треугольник.
Известно правило : катет лежащий напротив угла 30градусов равен половине гипотенузы. Значит этот катет равен ME/2=5.
а) EP найдем через теорему Пифагора :
EP^{2}=EM^{2}-PM^{2}
EP^{2}=100-25
EP^{2}=75
EP=корень из 75
EP находится в промежутке от 8 до 9.
б) В прямоугольном треуголнике медиана, проведенная к гипотенузе равна 0,5 гипотенузы.
Значит PM=EM/2
PM=10/2
PM=5
Обратим внимание на то, что в треугольнике MЕР, угол EMP равен 90 градусов, а угол MEP равен 30 градусов. Зная эти углы, можем утверждать, что треугольник MЕР - прямоугольный треугольник.
Мы знаем, что сторона ЕМ равна 10 см. Так как треугольник MЕР является прямоугольным, то мы можем использовать теорему Пифагора, чтобы найти длину стороны РМ.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы (в данном случае стороны МР) равен сумме квадратов длин других двух сторон (в данном случае стороны МЕ и МР).
Таким образом, мы можем записать формулу:
МР² = МЕ² + ЕР²
Мы знаем, что МЕ = 10 см, следовательно, можем подставить это значение в формулу:
МР² = 10² + ЕР²
Теперь осталось узнать длину стороны ЕР. Нам дано, что угол MEP равен 30 градусов. Мы знаем, что сумма углов треугольника равна 180 градусов, а значит угол ЕРМ равен 180 - 90 - 30 = 60 градусов.
Мы можем использовать формулу косинусов, чтобы найти длину стороны ЕР:
cos(60) = ЕР/10
Раскроем формулу:
1/2 = ЕР/10
Умножим обе части уравнения на 10, чтобы избавиться от дроби:
ЕР = 5
Теперь, когда мы знаем длину стороны ЕР, можем подставить это значение в формулу для МР:
МР² = 10² + 5²
МР² = 100 + 25
МР² = 125
Чтобы найти длину стороны МR, извлекаем квадратный корень из обеих частей уравнения:
МР = sqrt(125)
МР ≈ 11,2 см
Таким образом, длина отрезка РМ составляет примерно 11,2 см.