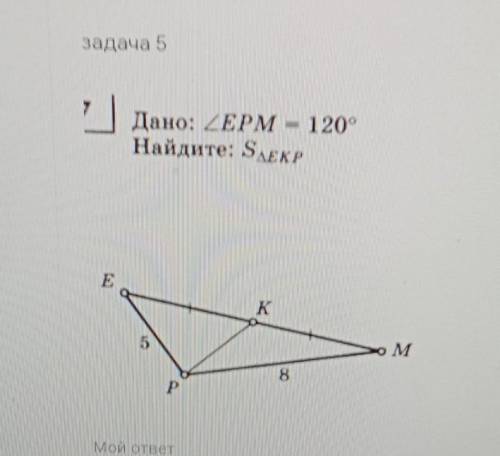
Дано: EPM = 120°
Найдите: S EKP​

S=0.5×S(EPM)
0.510×16*SIN120=40*(корень с 3)

Для решения данной задачи нам необходимо использовать знания по геометрии треугольника.

В данном случае у нас имеется треугольник EKP, в котором известна мера угла EPM, равная 120°.

Для нахождения площади треугольника EKP нам необходимо знать длину его основания и высоту, опущенную на это основание.

По изображению видно, что EG является высотой, опущенной на основание KP.

Таким образом, нам нужно найти длину основания KP и высоту EG.

Для нахождения KP нам необходимо знать длины сторон треугольника EKP, которые в данной задаче неизвестны. Без этих данных мы не можем точно определить длину основания KP.

Теперь обратимся к высоте EG. Заметим, что у нас дан угол EPM, который в данном случае является основанием для высоты EG. Зная меру этого угла, мы можем сказать, что EG является биссектрисой этого угла, а значит, делит его пополам. То есть, мера угла EGM будет равна половине 120°, то есть 60°.

Теперь, зная меру угла EGM, мы можем использовать тригонометрическую функцию тангенса для определения отношения длин сторон EG и GM.

Тангенс угла EGM равен отношению противолежащего катета EG к прилежащему катету GM. То есть, можно записать:

tan(EGM) = EG / GM

Подставим известные значения:

tan(60°) = EG / GM

Тангенс 60° равен √3, поэтому:

√3 = EG / GM

Перенесем GM на другую сторону уравнения:

EG = √3 * GM

Осталось найти длину EG и GM.

Здесь нам уже не хватает информации о длинах сторон треугольника EKP, поэтому дальнейшее решение задачи невозможно.

Итак, чтобы найти площадь треугольника EKP, нам нужна информация о длинах его сторон.