Дано: EF || AC, AE = EO, CF = FО. Доказать: АО и СО — биссектрисы.
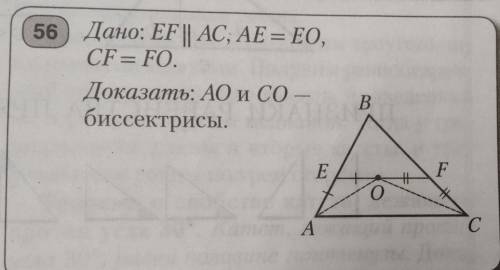
Другие вопросы по теме Геометрия
Популярные вопросы
- у кубі авсda, b, c, d задано точку: 1) р на ребрі аа,; 2) @ на ребрі...
2 - Скласти твір на тему Іноземні мови в житті сучасної молоді , 10-12...
2 - Задача на равнодействующую сил по Технической Механике...
3 - Вплив світла на ріст рослин?...
2 - Твір - роздум цілісніть здоров я...
3 - что ты делал летом рассказ на немецком(все как по примеру), пример:Ich...
2 - На прямой даны точки C D и D C? А лучи C D и D C?...
1 - Х+3х+5=17И 3, 5х+2,2х=4,56...
2 - Фонетический разбор слова съехать...
1 - Переведите в обыкновенную дробь 0,125 с объяснением . никак не пойму...
2
Дано:
EF || AC - это значит, что отрезки EF и AC параллельны.
AE = EO - это значит, что отрезки AE и EO равны по длине.
CF = FO - это значит, что отрезки CF и FO равны по длине.
Доказательство:
1. Мы знаем, что отрезки EF и AC параллельны, а значит, угол AEC и угол EFC - соответственные углы, и они равны (по их определению).
2. Также у нас есть два треугольника: треугольник AEF и треугольник CEF.
3. Мы знаем, что отрезки AE и EO равны по длине, а отрезки CF и FO равны по длине, а значит, эти треугольники равнобедренные (в них две стороны равны).
4. Значит, угол AFE равен углу CEF, так как они соответствующие углы в равнобедренных треугольниках.
5. Рассмотрим треугольник ABC. Так как EF || AC, то угол EAF равен углу ACF (параллельные прямые создают соответствующие углы).
6. Так как угол AEF равен углу CEF (равнобедренные треугольники), и угол EAF равен углу ACF (параллельные прямые), значит, угол AEF равен углу CEF.
7. То есть угол AEF равен углу CEF и угол AFE равен углу CFE. Это означает, что отрезки AO и CO делят угол на два равных угла (AO и CO являются биссектрисами).
Таким образом, мы доказали, что отрезки AO и CO являются биссектрисами.