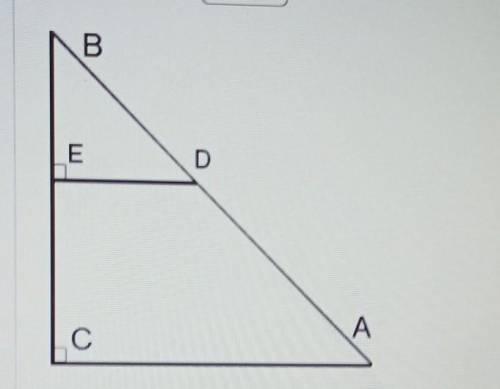
Дано: DBE ~ АВС,
CB = 48, DE = 3, AC = 15.
Найти: ВЕ​

Для начала разберемся с данными в условии задачи:

DBE ~ АВС означает, что треугольники DBE и АВС подобны.

CB = 48 означает, что отрезок CB равен 48.

DE = 3 означает, что отрезок DE равен 3.

AC = 15 означает, что отрезок AC равен 15.

Теперь перейдем к решению задачи. Нам нужно найти длину отрезка ВЕ.

Поскольку треугольники DBE и АВС подобны, мы можем использовать соотношение подобных треугольников, которое гласит:

AB/DB = AC/DE = BC/BE

Мы знаем значения AB, DB, AC, и DE, таким образом мы можем выразить BC/BE.

AB = AC + CB = 15 + 48 = 63

Теперь мы можем заменить значения в формуле и решить ее:

63/DB = 15/3 + 48/BE

63/DB = 5 + 48/BE

Теперь нам нужно найти DB и BE.

Мы не знаем DB, но мы можем найти его, используя теорему Пифагора в треугольнике DBE:

DB^2 = DE^2 + BE^2

DB^2 = 3^2 + BE^2

DB^2 = 9 + BE^2

Теперь мы имеем два уравнения с двумя неизвестными переменными DB и BE. Чтобы решить систему уравнений, мы можем подставить одно уравнение в другое и решить полученное уравнение.

Используя уравнение DB^2 = 9 + BE^2, мы можем подставить DB^2 = 9 + BE^2 в выражение 63/DB = 5 + 48/BE.

Теперь у нас есть одно уравнение с одной неизвестной переменной BE:

63/(9 + BE^2) = 5 + 48/BE

Теперь мы можем решить это уравнение:

63BE = (9 + BE^2)(5 + 48/BE)

63BE = 45 + 48(9 + BE^2)/BE

63BE = 45 + 48(9 + BE^2/BE)

63BE = 45 + 432/BE + 48BE

63BE - 48BE = 45 + 432/BE

15BE = 45 + 432/BE

15BE^2 - 45BE + 432 = 0

3BE^2 - 9BE + 96 = 0 (поделили все на 15)

Теперь мы имеем квадратное уравнение.

Используя формулу для нахождения корней квадратного уравнения, мы можем найти значение BE:

BE = (-(-9) ± √((-9)^2 - 4 * 3 * 96)) / (2 * 3)

BE = (9 ± √(81 - 1152)) / 6

BE = (9 ± √(-1071)) / 6

Поскольку внутри корня у нас отрицательное число, мы не можем получить реальные корни. Значит отрезок BE не может быть рассчитан с использованием данных, представленных в задаче.

Ответ: Данная задача не имеет решения с использованием предоставленных данных.