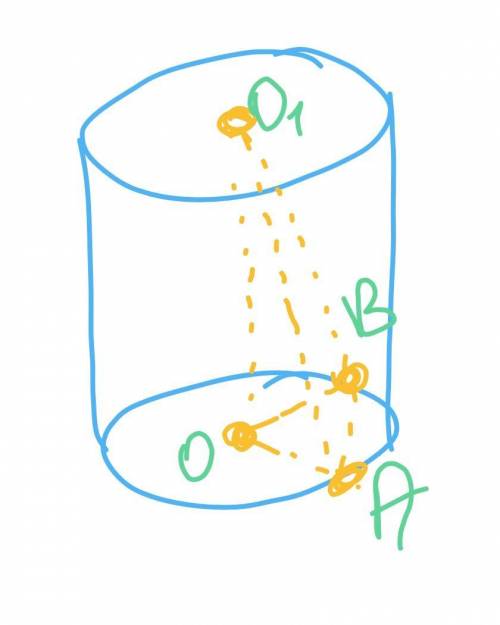
Дано: цилиндр, угол AO1B=60°, AB=15 см, ОА=9 см;
Найти: S бок.​

таоаоалалвлдвжвжвєвє

Для начала, давайте разберемся с терминами, которые используются в этой задаче. Цилиндр - это трехмерная геометрическая фигура, у которой основание является кругом, а боковая поверхность состоит из параллельных окружностей. Угол AO1B - это угол между прилегающими сторонами, AB и O1B. AB - это диаметр основания цилиндра, а ОА - это радиус основания.

Теперь перейдем к решению задачи. Для того, чтобы найти площадь боковой поверхности (Sбок) цилиндра, необходимо знать его высоту и окружность основания.

Дано, что AB = 15 см и ОА = 9 см. Мы можем найти радиус основания цилиндра, используя формулу радиуса ОА = радиус ( r ). Таким образом, r = 9 см.

Для нахождения площади боковой поверхности цилиндра, нам также необходимо найти окружность основания. Для этого, мы можем использовать формулу для длины окружности, где длина окружности ( C ) равна 2πr, где π - это математическая константа, приближенное значение которой равно 3.14. Таким образом, длина окружности C = 2πr.

Для нашего цилиндра, диаметр равен 15 см, следовательно радиус ( r ) равен половине диаметра, r = 15 / 2 = 7.5 см. Теперь, используя формулу длины окружности, мы можем вычислить C = 2πr = 2 * 3.14 * 7.5 = 47.1 см.

Теперь, когда у нас есть длина окружности, мы можем найти площадь боковой поверхности цилиндра. Формула для площади боковой поверхности ( Sбок ) цилиндра равна Sбок = C * h, где С - длина окружности, а h - высота цилиндра.

В задаче не дана высота цилиндра, поэтому нам нужно определить ее. Мы можем воспользоваться теоремой Пифагора для нахождения высоты.

Обозначим точку пересечения расширения высоты цилиндра (пунктирная линия, проведенная из вершины цилиндра) и продолжения стороны AB как точку C. Мы знаем, что в треугольнике ABC угол CAB = 60°, AC = 9 см и AB = 15 см.

По теореме Пифагора, сумма квадратов катетов (в нашем случае AC и BC) равна квадрату гипотенузы (AB), то есть AC^2 + BC^2 = AB^2. Подставляя известные значения, мы получаем 9^2 + BC^2 = 15^2, что приводит к уравнению 81 + BC^2 = 225. Перенося все известные значения на одну сторону, получаем BC^2 = 225 - 81 = 144.

Применим квадратный корень к обеим сторонам уравнения, чтобы найти BC: BC = √144 = 12 см.

Теперь мы знаем высоту цилиндра, которая равна BC = 12 см.

Возвращаясь к формуле для площади боковой поверхности, мы можем найти площадь, Sбок = C * h = 47.1 см * 12 см = 565.2 см^2.

Таким образом, площадь боковой поверхности цилиндра равна 565.2 см^2.