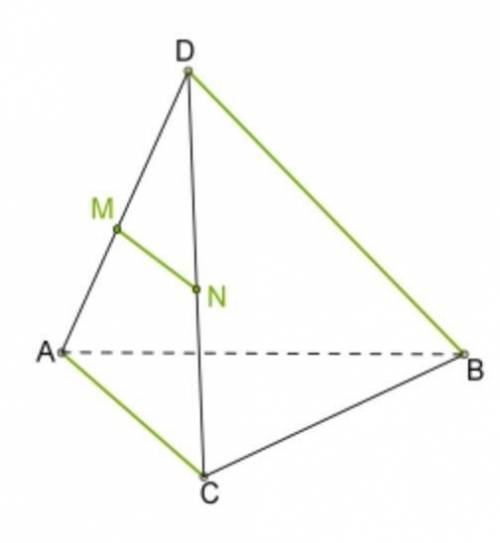
Дано, что в тетраэдре DABC ребро DB перпендикулярно ребру AC. На рёбрах DA и DC расположены серединные точки M и N. Докажи, что DB перпендикулярно MN.
1. Так как M и N — серединные точки DA и DC, то MN — треугольника ACD
2. Средняя линия ... третьей стороне треугольника, то есть AC.
3. Если DB перпендикулярна одной из ... прямых, то она
... и другой прямой.​

Для доказательства того, что ребро DB перпендикулярно MN, мы можем использовать следующий подход:

1. Пусть ребро DB пересекает линию MN в точке P. Нам необходимо доказать, что угол DPB равен 90 градусам.

2. Рассмотрим треугольники MAD и MCD. Поскольку точка M - серединная точка ребра DA, то DM равен половине ребра DA. Аналогично, MD равен половине ребра DC. Таким образом, треугольники MAD и MCD имеют равные стороны (DM = DM) и равные углы (по свойству серединных линий треугольника).

3. Следовательно, треугольники MAD и MCD равны по двум сторонам и углу (по критерию равенства двух треугольников).

4. Возьмем точку О - середину ребра DM. Так как О является серединной точкой, то OM равно половине ребра DM.

5. Теперь рассмотрим треугольники BOD и BOP. Мы знаем, что DB перпендикулярно AC. Поскольку AC является диагональю грани ACD тетраэдра, то DB является высотой этого треугольника.

6. В треугольнике BOD угол BDO является прямым, поскольку DB является высотой треугольника. Также у нас есть равные стороны OB и OD (по свойству серединной линии треугольника). Следовательно, треугольники BOD и BDO равны по стороне и двум углам (по первой теореме равных треугольников).

7. Из этого следует, что угол BOD равен углу BDO.

8. Теперь рассмотрим треугольники BOP и MOP. У них есть две равные стороны (OP является общей и BO равна MO), а также равные углы BOP и MOP (по теореме о равных треугольниках). Следовательно, треугольники BOP и MOP равны по двум сторонам и углу.

9. Из равенства треугольников BOP и MOP следует, что угол PBO равен углу PMO.

10. Таким образом, у нас есть две пары равных углов: BDO и PMO, а также BOP и MOP.

11. Из этого следует, что углы BDO и BOP являются вертикальными углами, так как они равны соответственно углам PMO и MOP.

12. Вертикальные углы равны по определению, поэтому BDO и BOP равны.

13. Но мы также установили, что BDO и BOP различаются на 90 градусов, так как BDO является прямым углом.

14. Следовательно, угол BOP равен 90 градусам.

15. Поскольку угол BOP равен 90 градусам, а угол PBO равен углу PMO, то угол PMO также равен 90 градусам.

16. Отсюда можно сделать вывод, что DB перпендикулярно MN, так как у них есть общий перпендикулярный угол PMO.

Таким образом, мы доказали, что ребро DB перпендикулярно линии MN.