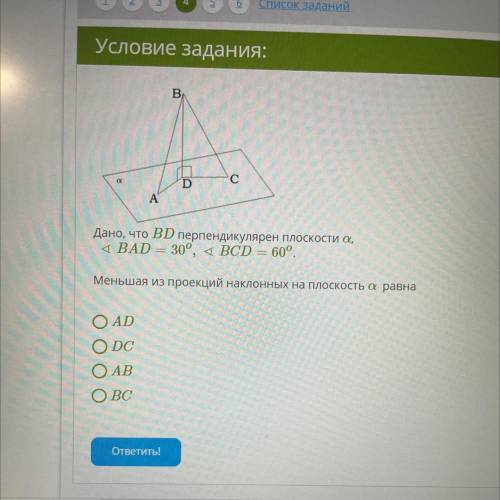
Дано, что BD перпендикулярен плоскости α,
∢BAD=30o,∢BCD=60o.

Меньшая из проекций наклонных на плоскость α равна

Для решения данной задачи нам необходимо рассмотреть геометрическую ситуацию.

Из условия задачи у нас имеется перпендикуляр BD к плоскости α и два угла ∠BAD = 30° и ∠BCD = 60°.

Обозначим точку пересечения прямой BD с плоскостью α как точку А'. Тогда мы можем нарисовать треугольник BAD, в котором BD является высотой.

Далее нарисуем перпендикуляр к BD, проходящий через точку А'. Обозначим точку пересечения этого перпендикуляра с прямой BC как точку C'.

Теперь у нас имеется треугольник BCD, в котором BD также является высотой, а BC - основанием.

По определению, проекцией наклонной на плоскость является высота треугольника, проведенная из вершины к основанию. Значит, проекции AC' и A'C являются проекциями наклонных AB и BA, соответственно.

Так как BD является высотой в треугольниках BAD и BCD, то длина проекций AC' и A'C будет равна расстоянию от точки A' до соответствующих сторон треугольников.

Мы знаем, что ∠BAD = 30° и ∠BCD = 60°. Заметим, что треугольники BAD и BCD являются подобными, так как углы ΔBAD и ΔBCD равны между собой и у них есть общий угол ∠B. Поэтому соответствующие стороны этих треугольников пропорциональны.

Обозначим длину проекции AC' как х. Тогда длина проекции A'C будет равна 2х, так как С является основанием треугольника BCD, а А - противолежащим углом к основанию. Таким образом, длина проекции A'C' будет равна 2х.

Теперь мы можем составить пропорцию:

AB / BC = AC' / A'C.

Из условия, AB = 10. Также у нас есть угол ∠BAD = 30°. Из пропорции треугольников BAD и BCD, получаем:

AC' / A'C = BD / BC,

BD = AB * sin(∠BAD) = 10 * sin(30°) = 5.

Так как BD является высотой, а BC - основанием, то BD / BC = AC' / A'C. Подставляя известные значения:

5 / BC = AC' / (2x).

Получаем пропорцию:

5 / BC = AC' / (2x).

Для нахождения длины проекции AC' нам необходимо найти длину стороны BC. Для этого воспользуемся теоремой синусов в треугольнике BCD:

sin(∠BCD) = BC / BD.

Подставляя известные значения, получаем:

sin(60°) = BC / 5.

Решая данное уравнение, находим:

BC = 5 * sin(60°) = 5 * (√3 / 2) = (5√3) / 2.

Теперь мы можем подставить найденную длину основания BC в пропорцию:

5 / ((5√3) / 2) = AC' / (2x).

Решаем данную пропорцию:

10 / (5√3) = AC' / (2x).

Для удобства и краткости записи обозначим √3 как k:

10 / (5k) = AC' / (2x).

Перемножим обе части пропорции на (5k * 2x), чтобы избавиться от знаменателя в левой части:

10 * 5k * 2x / (5k) = AC'.

Упрощаем выражение:

20x = AC'.

Таким образом, длина проекции AC' равна 20x.

Ответ: меньшая из проекций наклонных на плоскость α равна 20x.