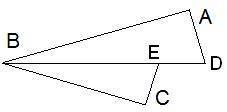
Дано, что BD — биссектриса угла CBA. BA⊥DAиCB⊥EC.
Вычисли CB, если DA= 9 см, BA= 12 см, EC= 4,5 см.
Сначала докажем подобие треугольников. (В каждое окошечко впиши одну латинскую букву или число.)
∢A=∢
=
°∢C
E=∢D
A,т.к.BE− биссектриса}⇒ΔADB∼ΔCEB по двум углам (по первому признаку подобия треугольников).
CB=
см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Відреагуйте речення Через пару днів 1 травня...
2 - 1. Подобрать заголовок. 2. Выделить в тексте ССК и определить их...
3 - 1. That red and blue top is very . ourclluof 2. Неr hair isn t straight...
3 - Доказать тождество sin(пи-a)cos(пи/2-a)+cos(2пи-a)sin(пи/2-a)...
3 - сократить дроби по образцу:...
3 - Шесть девочек: Маша, Вера, Таня, Света, Лена и Ира гуляли по улице...
3 - Упр 6 стр 117 Задать 5 общих во и 5 специальных во с данными словосочетаниями...
1 - При якому значенні a система рівнянь. {3x+ay=4,6x-2y=12 Розв язання...
2 - В каком варианте ответа указаны все слова, где пропущена буква Е?...
2 - Стехиометрическое соотношение компонентов при горении метана на...
3
Дано:
- BD - биссектриса угла CBA
- BA⊥DA (знак ⊥ означает перпендикулярность)
- CB⊥EC
Теперь рассмотрим треугольник ADB и треугольник CEB. Мы хотим доказать, что эти треугольники подобны друг другу.
Для начала, обратим внимание на углы. Из информации о биссектрисе мы знаем, что угол ADB равен углу CEB (обозначим их как ∢A и ∢C соответственно). Также, углы ∢D и ∢E в треугольниках ADB и CEB соответственно равны. Это связано с тем, что биссектриса делит угол пополам.
Таким образом, мы можем заключить, что треугольники ADB и CEB подобны друг другу по первому признаку подобия треугольников (УУ).
Теперь, используя подобие треугольников, можем записать пропорцию между сторонами треугольников:
AD/CE = AB/CB
Подставляя известные значения, получим:
9/4.5 = 12/CB
Выполняя вычисления, получаем:
2 = 12/CB
Теперь найдем CB, изолируя его в данном уравнении:
CB = 12/2
CB = 6 см
Таким образом, длина CB равна 6 см.