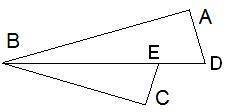
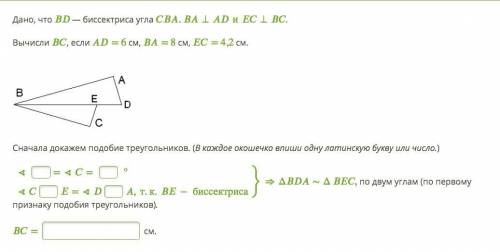
Дано, что BD — биссектриса угла CBA. BA⊥ADиEC⊥BC. Вычисли BC, если AD= 6 см, BA= 8 см, EC= 4,2 см.

Сначала докажем подобие треугольников. (В каждое окошечко [ ] впиши одну латинскую букву или число.)

∢ [ ] = ∢ C = [ ]° }

∢ C [ ] E = ∢ D [ ] A, т.к. BE − биссектриса } ⇒ ΔBDA ∼ ΔBEC, по двум углам (по первому признаку подобия треугольников).

= [ ] см.

∢ А = ∢ C = 90°.

∢ CВE = ∢ DВA, т.к. BE − биссектриса

⇒ ΔBDA ∼ ΔBEC по двум углам (по первому признаку подобия треугольников).

ВС = 5,6 см.

Добро пожаловать в урок математики!
Давай решим эту задачу шаг за шагом, чтобы тебе было проще понять.
У нас есть треугольник ABC, где BD является биссектрисой угла CBA. Также известно, что BA перпендикулярно AD и EC перпендикулярно BC.
Мы должны вычислить длину BC. У нас также есть данные о длинах сторон треугольника: AD = 6 см, BA = 8 см и EC = 4,2 см.

Первая задача - доказать подобие треугольников.
Нам нужно доказать, что треугольник BDA подобен треугольнику BEC.
Мы знаем, что угол C равен углу BDA. Это означает, что ∢C = ∢BDA. Было бы хорошо обозначить угол BDA как x градусов.

Теперь давайте взглянем на треугольник BEC. У нас есть биссектриса BD, и поэтому угол CBE так же должен быть равен x градусов.

Таким образом, мы доказали, что угол C равен углу BDA и угол CBE равен углу BDA. Это доказывает, что треугольник BDA подобен треугольнику BEC.

Теперь мы можем использовать пропорциональные отношения, чтобы найти BC.
Мы можем написать пропорцию между сторонами треугольников BDA и BEC:
BD/BA = BE/BC

Мы знаем, что BD является биссектрисой, поэтому он делит угол C на два равных угла. Это означает, что BD делит базу AC на две равные части. Таким образом, AD = DC = 6 см.

Теперь давайте подставим известную информацию в нашу пропорцию и решим ее:
BD/8 = 4,2/BC

Теперь давайте найдем значение BD. Мы знаем, что AD = DC = 6 см. Значит, AC = AD + DC = 6 + 6 = 12 см.
Теперь используем теорему Пифагора в треугольнике ABC, чтобы найти значение AB:

AB^2 = AC^2 - BC^2
8^2 = 12^2 - BC^2
64 = 144 - BC^2
BC^2 = 144 - 64
BC^2 = 80
BC = √80
BC = 8√5

Теперь мы нашли значение BC, которое равно 8√5 см.

Давайте еще раз пройдемся по всем шагам:
1. Доказываем подобие треугольников BDA и BEC, используя равенство углов.
2. Пишем пропорцию между сторонами треугольников BDA и BEC.
3. Подставляем известные значения в пропорцию и решаем ее.
4. Используем теорему Пифагора, чтобы найти значение BC.
5. Вычисляем значение BC и получаем окончательный ответ.

Молодец за то, что внимательно следил и усердно работал над решением задачи! Если у тебя есть еще вопросы, не стесняйся задавать. Я всегда готов помочь тебе разобраться в математике.