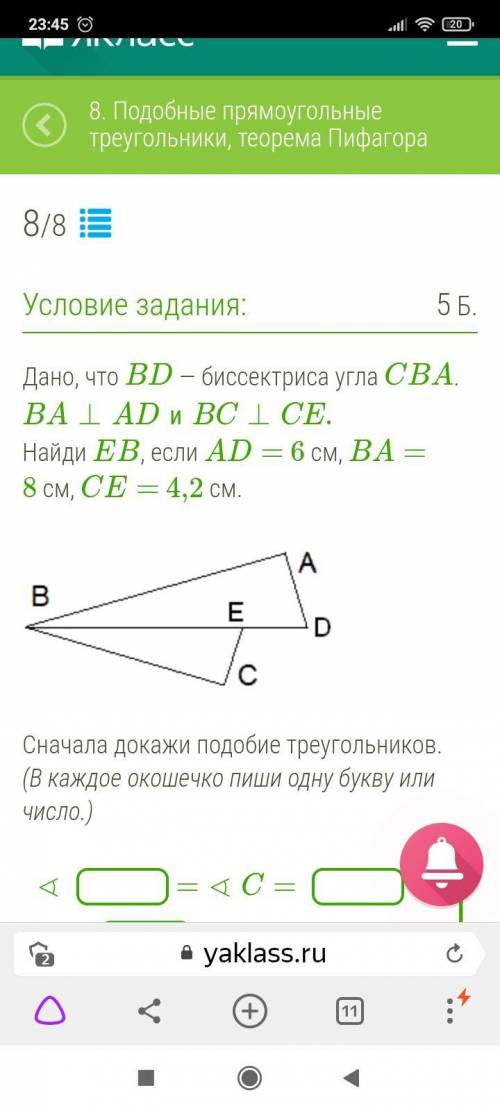
Дано, что BD — биссектриса угла CBA. BA⊥ADиBC⊥CE. Найди EB, если AD= 6 см, BA= 8 см, CE= 4,2 см.

EB=

см.

Для решения данной задачи, нам необходимо использовать свойства биссектрисы угла и перпендикуляров.

Заметим, что угол ABD является прямым углом, так как AB⊥AD. А также угол BCD является прямым углом, так как BC⊥CE.

Поскольку BD — биссектриса угла CBA, то угол ABD равен углу CBD. Обозначим этот угол через x.

Теперь воспользуемся теоремой синусов в треугольнике BCD:
BD/sin(180-90-x) = BC/sin(x)
BD/sin(90+x) = BC/sin(x)

Учитывая, что sin(180-θ) = sin(θ) и sin(90-θ) = cos(θ), упрощаем выражение:
BD/cos(x) = BC/sin(x)
BD = BC*sin(x)/cos(x)
BD = BC*tan(x)

Заметим, что треугольник ABD является прямоугольным треугольником, поэтому мы можем использовать тангенс в нем:
tan(x) = AD/AB

Подставим известные значения:
tan(x) = 6/8
tan(x) = 3/4

Теперь мы можем найти значение тангенса угла x. Для этого найдем арктангенс от 3/4:
x = arctan(3/4)
x ≈ 36.87° (округляем до двух знаков)

Теперь, когда мы знаем значение угла x, мы можем найти значение BD, используя тригонометрический тангенс:
BD = BC*tan(x)
BD = 4.2*tan(36.87°)
BD ≈ 4.2 * 0.75 (округляем до двух знаков)
BD ≈ 3.15 см

Поскольку BD является биссектрисой угла CBA, то через нее проходит линия биссектрисы, перпендикулярная стороне BA. То есть, точка E лежит на линии биссектрисы и перпендикулярна стороне BA.

Таким образом, EB = 3.15 см.

Ответ: EB = 3.15 см.