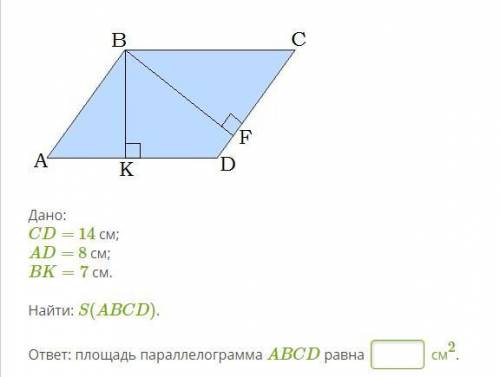
Дано:
CD= 14 см;
AD= 8 см;
BK=7 см.

Найти: S(ABCD)

Чтобы решить эту задачу, мы можем использовать такие понятия, как площадь прямоугольника и свойства прямоугольников.

Площадь прямоугольника вычисляется по формуле S = a * b, где a и b - это длины двух сторон прямоугольника.

Дано: CD = 14 см, AD = 8 см, BK = 7 см.

Нам нужно найти площадь прямоугольника ABCD. Воспользуемся формулой для площади прямоугольника S = a * b.

Для этого нам нужно найти длины сторон AB и BC.

1. Посмотрим на треугольник ADC. У нас есть две известные стороны: CD = 14 см и AD = 8 см. Мы можем воспользоваться теоремой Пифагора, чтобы найти третью сторону AC.

AC^2 = AD^2 + CD^2
AC^2 = 8^2 + 14^2
AC^2 = 64 + 196
AC^2 = 260
AC = √260
AC ≈ 16.12 см

2. Теперь у нас есть сторона AC, а также сторона BK = 7 см. Нам нужно найти сторону BC.

BC = AC - BK
BC = 16.12 - 7
BC ≈ 9.12 см

3. Теперь, когда у нас есть стороны AB и BC, мы можем найти площадь прямоугольника ABCD, используя формулу S = a * b.

S(ABCD) = AB * BC
S(ABCD) ≈ 9.12 * 16.12
S(ABCD) ≈ 146.97 см²

Итак, площадь прямоугольника ABCD составляет около 146.97 квадратных сантиметров.