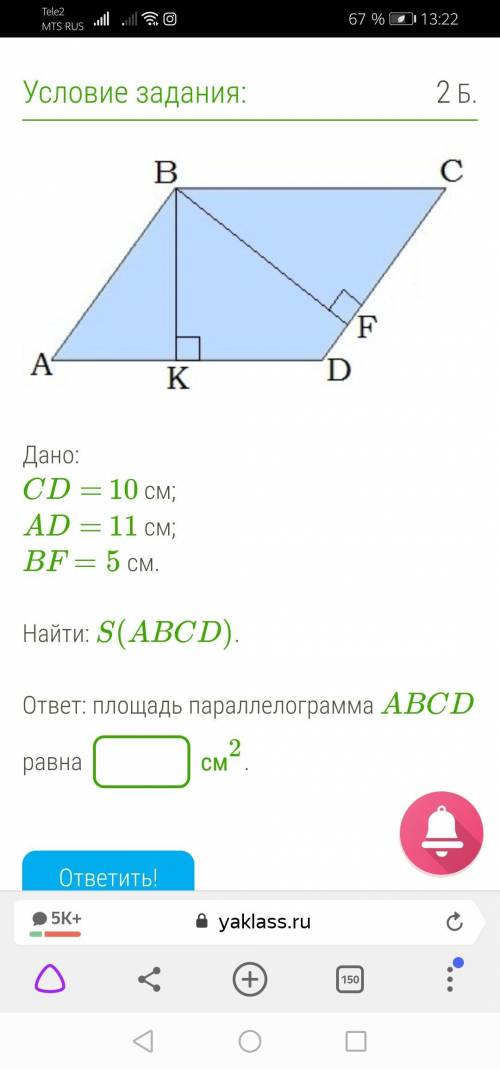
Дано: CD= 10 см;
AD= 11 см;
BF=5 см.
Найти: S(ABCD).
ответ: площадь параллелограмма ABCD равна ? См2
Другие вопросы по теме Геометрия
Популярные вопросы
- Who had the fastest lap?the table below...
2 - Поставь глаголы в время, запиши предложения и переведи на русский язык 1) I (eat)...
2 - 2 Письменно Подготовка к СОР(продолжение)Прочитайте сказку «Солнце и туча» ДжанниРодари...
3 - . Complete the questions with do or does....
3 - Https://arizonawet.arizona.edu/users/free-watch-chal-mera-putt-2-2020-full-movie-online-0...
3 - Площадь плота, изготовленного из сосновых брусьев квадратного сечения, равна 4...
3 - Таблица голосеменных растений города(ель,сосна, лиственница)...
3 - Найти сходство и различия из произведения Русалочка...
2 - 5 предложений с использование слов речевого этикета?...
3 - Прочитайте документ и ответьте на во Из воспоминаний А.А. Брусилова. «Наступление...
3
Для начала, нам нужно найти высоту параллелограмма. Чтобы это сделать, нам понадобятся данные о треугольниках внутри параллелограмма.
Мы можем заметить, что треугольник ADC является прямоугольным, так как сторона CD - диаметр окружности, а диагональ AC - гипотенуза. Следовательно, мы можем использовать теорему Пифагора, чтобы найти длину стороны AC.
Используем теорему Пифагора:
AC^2 = AD^2 + CD^2
AC^2 = 11^2 + 10^2
AC^2 = 121 + 100
AC^2 = 221
Теперь найдем длину стороны AC, взяв квадратный корень из полученного значения:
AC = √221
Далее, нам нужно найти высоту параллелограмма. Мы можем использовать свойства параллелограмма, чтобы понять, что высота лежит на перпендикулярной стороне AB.
Можно также заметить, что треугольник ABF также является прямоугольным. Мы можем использовать теорему Пифагора, чтобы найти высоту BF.
Используем теорему Пифагора:
BF^2 = AB^2 - AF^2
BF^2 = AB^2 - (AD - BF)^2
BF^2 = AB^2 - (11 - 5)^2
BF^2 = AB^2 - 6^2
BF^2 = AB^2 - 36
Мы также знаем, что BF = 5 см, поэтому мы можем записать:
5^2 = AB^2 - 36
25 = AB^2 - 36
AB^2 = 25 + 36
AB^2 = 61
Теперь найдем длину стороны AB, взяв квадратный корень из полученного значения:
AB = √61
Итак, мы получили длину сторон AB и AC, и можем найти площадь параллелограмма.
S(ABCD) = AB * h = AB * BF
S(ABCD) = √61 * 5
Таким образом, площадь параллелограмма ABCD равна примерно 75,77 см².