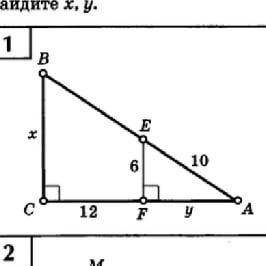
Дано: cba и fea cf=12; fe=6; es=10 найти cb и fa

Для решения этой задачи, нам необходимо использовать теорему Пифагора и некоторые свойства треугольников.

Мы видим, что в треугольнике FEA, сторона FE равна 6, а сторона ES равна 10. Чтобы найти сторону FA, мы можем использовать теорему Пифагора, так как у нас есть данные о двух сторонах треугольника.

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат гипотенузы (в нашем случае сторона FA) равен сумме квадратов двух катетов (FE и ES). Таким образом, мы можем записать это в формуле:

FA^2 = FE^2 + ES^2
FA^2 = 6^2 + 10^2
FA^2 = 36 + 100
FA^2 = 136

Теперь мы можем найти значение FA, взяв квадратный корень из обеих сторон:

FA = sqrt(136)

Мы не можем найти точное значение для FA, но можем упростить его. Мы видим, что 136 делится на 4 без остатка, поэтому мы можем вынести за знак радикала 4:

FA = sqrt(4 * 34)
FA = 2 * sqrt(34)

Таким образом, значение FA равно 2 * sqrt(34).

Теперь давайте рассмотрим треугольник CBA. У нас есть информация о стороне CF, которая равна 12. Чтобы найти сторону CB, мы также можем использовать теорему Пифагора, так как у нас есть данные о двух сторонах.

Мы знаем, что сторона CBA является гипотенузой треугольника, а стороны CB и BA - это катеты. Теорема Пифагора говорит нам, что:

CB^2 = CF^2 + FB^2

Однако у нас нет никакой информации о стороне FB. Но мы можем заметить, что сторона FB является подотрезком стороны FA, то есть FB = FA - CB.

Теперь мы можем переписать формулу для нахождения CB с использованием этих заметок:

CB^2 = CF^2 + (FA - CB)^2

Раскроем это:

CB^2 = CF^2 + FA^2 - 2 * FA * CB + CB^2

Теперь мы можем объединить члены, содержащие CB:

0 = CF^2 + FA^2 - 2 * FA * CB

Перенесем все к одной стороне уравнения:

2 * FA * CB = CF^2 + FA^2

CB = (CF^2 + FA^2) / (2 * FA)

Подставив значения CF и FA, которые мы уже рассчитали, мы можем найти значение CB:

CB = (12^2 + (2 * sqrt(34))^2) / (2 * 2 * sqrt(34))
CB = (144 + 4 * 34) / (4 * sqrt(34))
CB = (144 + 136) / (4 * sqrt(34))
CB = 280 / (4 * sqrt(34))
CB = 70 / sqrt(34)
CB = (70 / sqrt(34)) * (sqrt(34) / sqrt(34)) [раскроем знаменатель]
CB = (70 * sqrt(34)) / 34
CB = 35 * sqrt(34) / 17

Таким образом, значение CB равно 35 * sqrt(34) / 17.

Итак, мы получили значения для сторон CB и FA в данной треугольной задаче:
CB = 35 * sqrt(34) / 17
FA = 2 * sqrt(34)