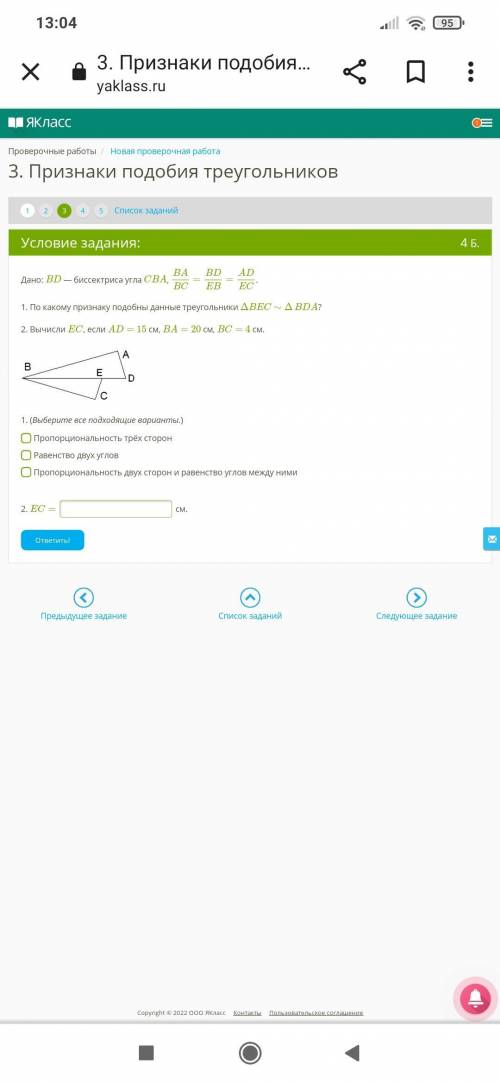
Дано: BD - биссек. угла CBA, BA/BC=BD/EB=AD/EC 1.по какому признаку подобны данные треугольники ∆BEC ~∆BDA ?

2.вычесли EC, если AD=15см ,BA=20см, BC=4см

ec=см?

Для того чтобы понять, по какому признаку данные треугольники подобны, нужно рассмотреть условие данной задачи.

Из условия дано, что BD - биссектриса угла CBA, и что отношение сторон треугольников ∆BEC и ∆BDA составляет: BA/BC = BD/EB = AD/EC.

1. Определение подобия треугольников:
Треугольники ∆BEC и ∆BDA будут подобны, если углы ∠BEC и ∠BDA равны (по теореме о биссектрисе угла), а отношение соответствующих сторон равно данному отношению.

2. Рассмотрение отношений длин сторон:
Из условия дано: BA/BC = BD/EB = AD/EC.
По данному отношению, можем выразить EB и EC:
BA/BC = BD/EB => EB = (BC * BD) / BA.
BD/EB = AD/EC => EC = (EB * AD) / BD.

Подставим значения из условия:
BA = 20 см, BC = 4 см, AD = 15 см.
Возьмем в расчет, что BD = x (длина биссектрисы).

Тогда, EB = (4 * x) / 20 = x / 5.
Подставляем данное значение EB во второе уравнение:
EC = ((x / 5) * 15) / x = 3.

Таким образом, получаем, что EC = 3 см.

Итак, пошагово решая задачу, мы определили, что треугольники ∆BEC и ∆BDA подобны по признаку равных углов и одинаковых отношений длин сторон. При данных длинах сторон AD = 15 см, BA = 20 см и BC = 4 см, мы посчитали длину EC, которая составляет 3 см.