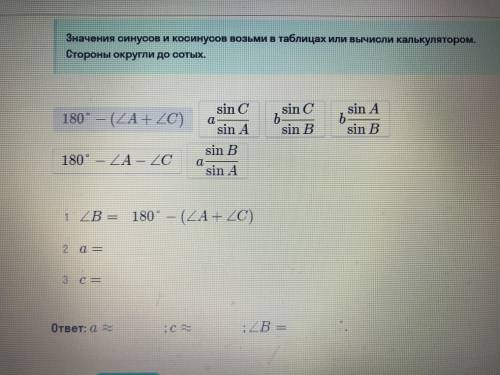
Дано:b=4,угол А=37 градусов, угол С =78 градусов.Найти а,с,угол В. Значение синусов и косинусов возьми в таблице или вычески калькулятором.Стороны округли до сотых.

Для решения данной задачи, воспользуемся теоремой синусов для треугольников.

Согласно теореме синусов, отношение длины стороны треугольника к синусу противолежащего угла равно одному и тому же отношению для других сторон треугольника:
a/sin(A) = b/sin(B) = c/sin(C)

В данной задаче известна сторона b и углы А и С. Мы должны найти стороны a и c, а также угол В.

1. Найдем сторону a:
Используем формулу теоремы синусов для стороны a:
a/sin(A) = b/sin(B)

Подставляем известные значения:
a/sin(37) = 4/sin(B)

Переносим sin(B) в левую часть уравнения и переносим sin(37) в правую часть:
a = (4 * sin(37)) / sin(B)

Округляем результат до сотых:
a = (4 * 0.6018) / sin(B)
a = 2.4072 / sin(B)

2. Найдем сторону c:
Используем формулу теоремы синусов для стороны c:
c/sin(C) = b/sin(B)

Подставляем известные значения:
c/sin(78) = 4/sin(B)

Переносим sin(B) в левую часть уравнения и переносим sin(78) в правую часть:
c = (4 * sin(78)) / sin(B)

Округляем результат до сотых:
c = (4 * 0.9781) / sin(B)
c = 3.9124 / sin(B)

3. Найдем угол В:
Используем формулу теоремы синусов для угла В:
a/sin(A) = b/sin(B) = c/sin(C)

Подставляем известные значения:
2.4072 / sin(37) = 4/sin(B) = 3.9124 / sin(78)

Из полученного уравнения можно выразить sin(B):
sin(B) = (4 * sin(37)) / 2.4072

Округляем результат до сотых:
sin(B) = 0.6018

Находим угол В по значению sin(B) из таблицы или калькулятора, обратившись к обратному синусу:
B = arcsin(0.6018)

Округляем результат до градусов:
B = 36.67 градусов

Таким образом, ответ на вопрос:
a = 2.41 (округлено до сотых)
c = 3.91 (округлено до сотых)
Угол В = 36.67 градусов

балы дайте пожалуйста дайте балы мне нужн осрочно балы балы балы блаы балы